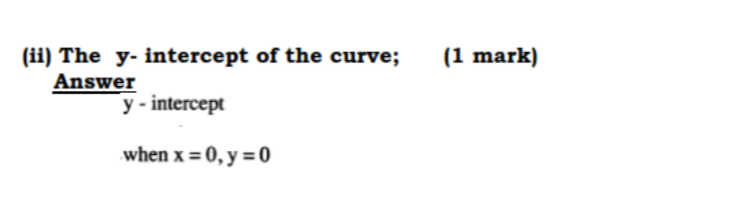KNEC KCSE Past Papers 2016 Kiswahili Paper 3 (102/3)
KCSE Past Papers 2016 Mathematics Alt A Paper 1
SECTION I (50 marks)
Answer all the questions from this section in the spaces provided
1. Without using a calculator evaluate, (3 marks)
2. Simplify
(4 marks)
3. The external length, width and height of an open rectangular container are 41 cm, 21 cm and 15.5 cm respectively.
The thickness of the materials making the container is 5mm. If the container has 8 litres of water, calculate the internal height above the water level. (4 marks)
4. The figure below shows a net of a solid (measurements are in centimetres).
Below is a part of the sketch of the solid whose net is shown above. Complete the sketch of the solid, showing the hidden edges with broken lines. (3 marks)
5. Given that OA = 2i + 3j and OB = 3i — 2j, find the magnitude of AB to one decimal place. (3 marks)
6. A bus travelling at an average speed of 63 km/h left a station at 8:15 a.m. A car later left the same station at 9:00 a.m. and caught up with the bus at 10:45 a.m. Find the average speed of the car. (3 marks)
7. Given that x is an acute angle and cos x° = 2/5 find, without using mathematical tables or a calculator, tan (90 — x)°. (2 marks)
8. Without using mathematical tables or a calculator, evaluate 272/3x(81/16)-1/4 (3 marks)
9. A minor arc of a circle subtends an angle of 105° at the centre of the circle. If the radius of the circle is 8.4 cm, find the length of the major arc. (Take IC = ). (3 marks) 10. The gradient of the tangent to the curve y = ax3 + bx at the point (1,1) is —5. Calculate the values of a and b. (4 marks)
11. A line with gradient of —3 passes through the points (3, k) and (k, 8). Find the value of k and hence express the equation of the line in the form ax + by = c, where a, b and c are constants. (3 marks)
12. Points L and M are equidistant from another point K. The bearing of L from K is 330°. The bearing of M from K is 220°.
Calculate the bearing of M from L. (3 marks)
13. in this question, mathematical tables should not be used. A Kenyan bank buys and sells foreign currencies as shown below:
1 Hong Kong Dollar 1 South African Rand
Buying (In Kenya Shillings) 9.74 12.03
Selling (In Kenya Shillings) 9.77 12.11
A tourist arrived in Kenya with 105 000 Hong Kong Dollars and changed the whole amount to Kenya Shillings.
While in Kenya, she spent Sh 403 879 and changed the balance to South African Rands before leaving for South Africa. Calculate the amount in South African Rand. that she received. (3 marks)
14. A small cone of height 8cm is cut off from a bigger cone to leave a frustum of height 16 cm. If the volume of the smaller cone is 160 cm’.
find the volume of the frustum. (3 marks) 15. The production of milk, in litres, of 14 cows on a certain day was recorded as follows:
22, 26, 15, 19, 20, 16, 27, 15, 19, 22, 21, 20, 22 and 28. Determine:
(b) the median. (2 marks)
16. Given that Log 4 = 0.6021 and Log 6 = 0.7782, without using mathematical tables or a calculator, evaluate log 0.096. (3 marks)
SECTION 11 (50 marks)
Answer any five questions from this section in the spaces provided 17. (a) Solve the equation 3 — 1 24 x — 2 (4 marks)
(b) The length of a floor of a rectangular hall is 9m more than its width. The area of the floor is 136 m2.
(i) Calculate the perimeter of the floor.
(4 marks)
(ii) A rectangular carpet is placed on the floor of the wall leaving an area of 64 m2.
If the length of the carpet is twice its width. determine the width of the carpet. (2 marks)
18. Three business partners: Asha. Nangila and Cherop contributed Ksh 6 000, Ksh 85 000 and Ksh 105 000 respectively.
They agreed to put 25% of the profit back into business each year. They also agreed to put aside 40% of the remaining profit to cater for taxes and insurance.
The rest of the profit would then be shared among the partners in the ratio of their contributions.
At the end of the first year, the business realised a gross profit of Ksh 225 000.
(a) Calculate the amount of money Cherop received more than Asha at the end of the first year. (5 marks)
(b) Nangila further invested Ksh 25 000 into the business at the beginning of the second year. Given that the gross profit at the end of the second year increased in the ratio 10:9, calculate Nangila’s share of the profit at the end of the second year. (5 marks)
19. The frequency table below shows the daily wages paid to casual workers by a certain company.
(a) In the grid provided, draw a histogram to represent the above information. (5 marks)
(b) (i) State the class in which the median wage lies. (1 mark)
(ii) Draw a vertical line, in the histogram, showing where the median wage lies. ( 1 mark)
(c) Using the histogram, determine the number of workers who earn Sh 450 or less per day. (3 marks)
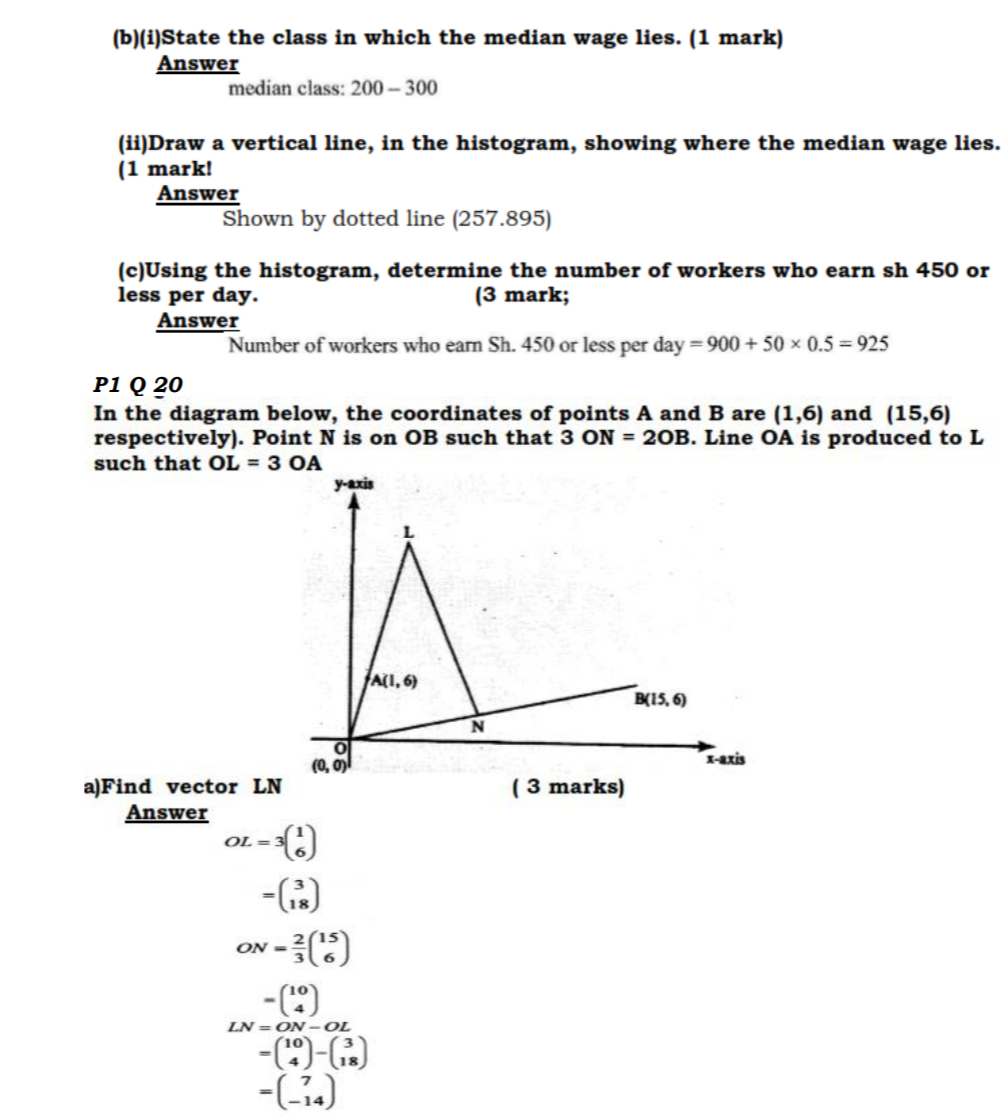
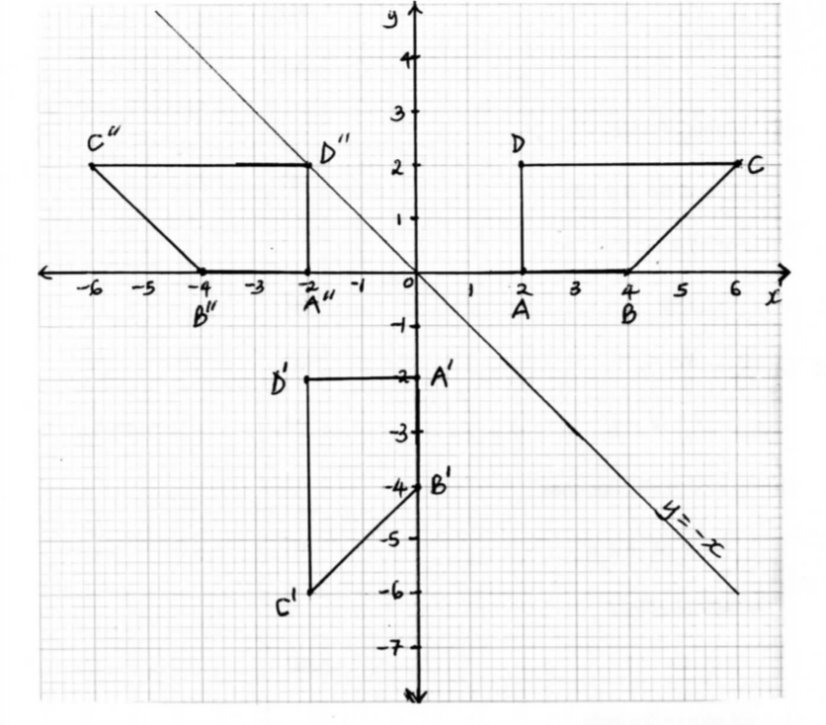
20. In the diagram below, the coordinates of points A and B are (1, 6) and (15, 6) respectively. Point N is on OB and that 30N = 20B. Line OA is produced to L such that OL = 30A
(a) Vector LN. (3 marks)
(b) Given that a point M is on LN such that LM:MN = 3:4, find the coordinate of M. (2 marks)
(c) If line OM is produced to T such that OM:MT = 6:1
(i) Find the position vector of T. (1 mark)
(ii) Show that points L, T and B are collinear. (4 marks)
21. (a) The ratio of Juma’s and Akinyi’s earnings was 5:3. Juma’s earnings rose to Ksh 8 400 after an increase of 12%.
Calculate the percentage increase in Akinyi’s earnings given that the sum of their new earnings was Ksh 14 100. (6 marks)
(b) Juma and Akinyi contributed all the new earnings to buy maize at Ksh 1175 per bag. The maize was then sold at Ksh 1762.50 per bag.
The two shared all the money from the sales of the maize in the ratio of their contributions.
Calculate the amount that Akinyi got. (4 marks)
22. Using a pair of compasses and ruler only, construct:
(a) (i) triangle ABC in which AB = 5cm, LBAC = 30° and LABC = 105°. (3 marks)
(ii) a circle that passes through the vertices of the triangle ABC. Measure the radius. (3 marks)
(iii) the height of triangle ABC with AB as the base. Measure the height. (2 marks)
(b) Determine the area of circle that lies outside the triangle correct to 2 decimal places. (2 marks)
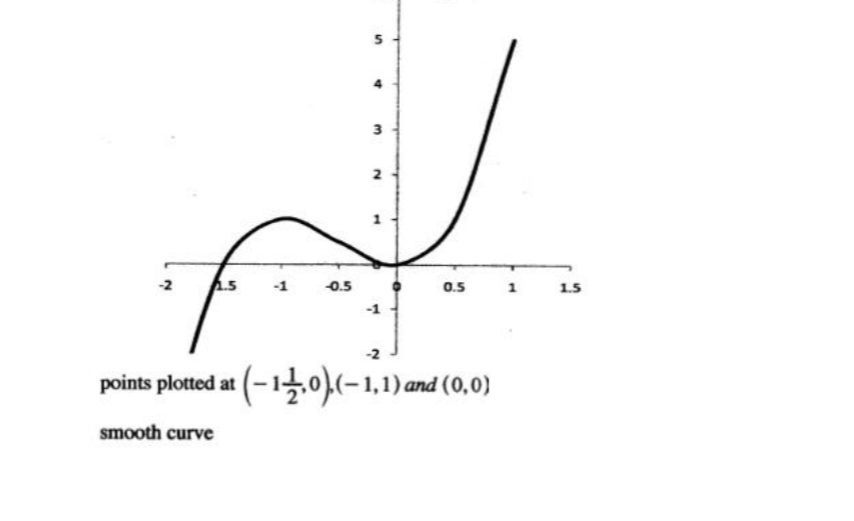
23. The equation of a curve is y = 2×3 + 3×2.
(a) Find:
(i) the x-intercept of the curve: (ii) the y-intercept of the curve. (1 mark)
(b) (i) Determine the stationary points of the curve. (2 marks)
(ii) For each point in (b)
(i) above, determine whether it is a maximum or a minimum. (2 marks)
(c) Sketch the curve. (2 marks)
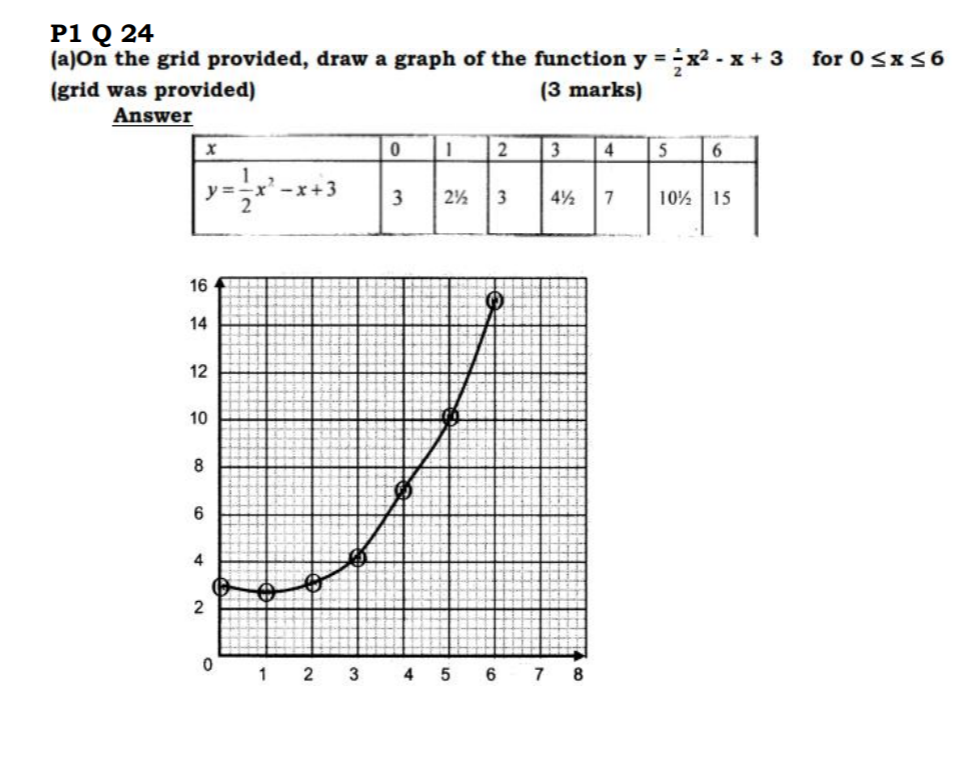
24. (a) On the grid provided, draw a graph of the function y = —2 x2 — x + 3 for 0 < x < 6. (3 marks)

Questions and Answers
2016 Mathematics Paper 1