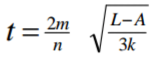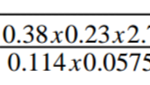KCSE Mathematics Paper 2 – 2014 EKSIKA Joint Evaluation Test
2014 EKSIKA Joint Evaluation Test
Mathematics Paper 2
SECTION I (50 Marks)
Answer ALL questions in this section.
Use logarithms only to evaluate,
Correct to four significant figures.
4 marks
Make k the subject of the formula.
3 marks
Express the recurring decimal below as a fraction; 4.372 leaving your answer in the
form of 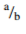
2 marks
Determine the amplitude, period and the phase angle of the wave represented by the equation.
3 marks
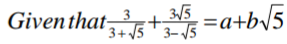
4 marks
The dimensions of a cuboid are 4.5cm by 3.5cm by 2cm.Find the percentage error in its volume giving your answer to 2 significant figure.
3 marks
A car was valued at kshs.500,000 in January 2010.Each year its value depreciated at12% p.a.After how long would the value depreciate to kshs.250,000?
3 marks
Given that the matrix 
2 marks
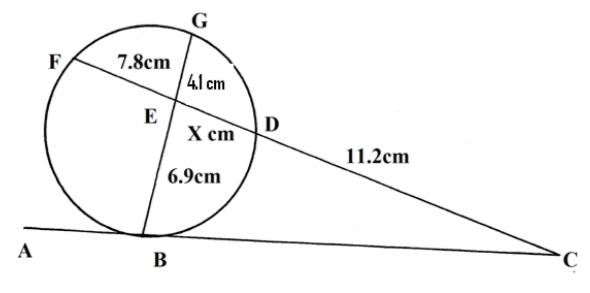
In the figure below ABC is a tangent to the circle at point B.Given that BE =6.9cm, FE=7.8cm, GE=4.1cm,DC=11.2cm and ED = xcm.Determine the length BC,give youranswer in four significant figures.
4 marks
Find the radius and the co-ordinates of the centre of the circle whose equation is
½ x2+ ½ y2 =3x – 5y – 9.
3 marks
A quantity P varies partly as t and partly as the square of t.When t = 20, p = 45 , and when t = 24 , p = 60.
(a) Express p in terms of t. (2mks)
(b) Find p when t = 32. (2mks)
4 marks
The position vectors of points A and B are a = 2i + j – 8k and b = 3i +2j – 2k respectively. Find the magnitude of AB.
3 marks
Write the expression of 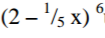
4 marks
Five men working 8 hours daily complete a piece of work in 3 days. How long will it
take 12men working 5hours a day to complete the same work.
2 marks
Find the integral values of x which satisfy 6 < 2x + 1 and 5x – 29 < – 4 .
3 marks
In a fund-raising committee of 45 people, the ratio of men to women is 7 : 2.Find the number of women required to join the existing committee so that the ratio of men to women changes to 5 : 4.
3 marks
SECTION II (50 Marks)
Attempt any five questions from this section
The table below gives the income tax rates.
| Income (k£) | Rate (p.a) |
| 1-1980 | 10% |
| 1981-3960 | 15% |
| 3961-5940 | 25% |
| 3941-7920 | 35% |
| 7921-8650 | 45% |
| Over 8651 | 50% |
(a) Calculate income tax of Wanga’s taxable income of kshs.50,400 per month allowing a family relief of kshs. 520 per month. (8mks)
(b) Calculate the total tax as a percentage of taxable income (2mks)
10 marks
(a) Draw ∆PQR whose vertices are P(1,1), Q(-3,2) and R(0,3) on the grid provided.
(b) Find and draw the image of ∆PQR under the transformation whose matrix is
P’Q’R’ is then transformed into P11 Q11 R11 by the transformation with the matrix 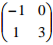
(c) Find the co-ordinates of P11 Q11 R11 and draw P11 Q11 R11(3mks)
(d) describe fully the single transformation which maps PQR onto P11 Q11R11 . Find the matrix of this transformation (3mks)
10 marks
The probability of passing K.C.P.E depends on performance in the school mock examination. If the candidate passes in mock, the probability of passing K.C.P.E is 4/5. If the candidate fails in mock, the probability of passing K.C.P.E is 3/5 .If the candidate passes K.C.P.E, the probability of getting employed is 1/3,the probability of passing mock is 2/3.:
(a). Draw a well label tree diagram to represent the above information(2mks)
(b) Use your tree diagram in (a) above to find the probability that she
i) Passes KCPE exams (2mks)
ii) Gets employed (2mks)
iii) Passes KCPE and gets employed (2mks)
iv) Passes mock and gets employed (2mks)
10 marks
The diagram below shows triangle O.A.B in which N is the mid point of AB.Mis apoint on OA such that OM :MA=2:1.Lines ON and BN meet at X such that vector OX=h vector ON and ,MX= kMB.
Given that vector OA =a and vector OB=b
(i) Express the following interms of a and b
(a) Vector AB (1mk)
(b) Vector ON (2mks)
(c) Vector BM ( 1mk)
(ii) By expressing vector OX in two different ways ,determine the values of h and k. (6mks)
10 marks
Using a ruler and a compass only
(a) Construct a parallelogram ABCD such that AB = 10cm BC=7cm and < ABC 105o(5mks)
(b) Construct the loci of P and Q within the parallelogram such that AP < 4cm and BQ < 6cm (2mks)
(c) Calculate the area within the parallelogram and outside the region bounded by the two loci (3mks)
10 marks
(a) Complete the table below.
| x | -30 | 0 | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 |
| Sin (x+30) | 0 | 0.50 | _ | 1.00 | 0.87 | _ | _ | -0.50 | _ | _ | -0.87 |
| Cos ( x-15) | 0.71 | _ | 0.97 | _ | 0.26 | _ | _ | _ | -0.97 | -0.71 | -0.26 |
(b) Draw the graph of y = sin (x+30) and y=cos(x-15) for -30≤X≤270o on the same grid. Take 1cm to represent 30o on x-axis and 1cm to represent 0.2units on y-axis.
Using your graph drawn (b) above
(i) Find the values of x for which cos (x-15) –sin (x+30) = 0 ( 2mks)
ii) State the co-ordinates of the turning point of the curvefor the function y =cos
(x-15) on the negative section of y-axis ( 1mk)
iii) Estimate the angle corresponding to cos (x-15) = 0.6
10 marks
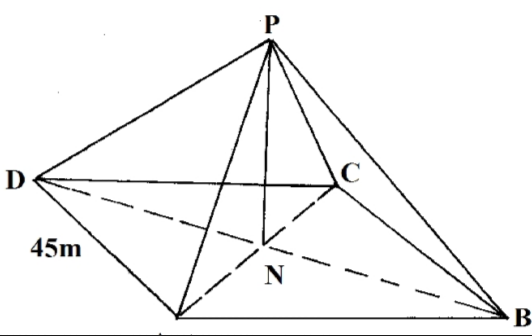
The figure below shows rectangular plot ABCD with AB =60m and BC=45m. PN is a vertical pole of length 30m to which four taut wire PB1, PC1,PD and PA are attached.
Calculate
(a) length of the projection of PCon the plane ABCD (2mrks)
(b) the angle PC made with the base ABCD (3mks)
(c) The angle between the planes PBC and ABCD (3Mrks)
(d) If point A is to be the North of point C. calculate the bearing of B from A (2mks)
10 marks
(a) The first term of an arithmetic progression (AP) is 2. The sum of the first 8 terms of AP is 256.
(i) Find the common difference of AP. (2mks)
(ii) Given that the sum of the first n terms of the AP 416. Find n. (2mks)
(b) The 3rd, 5th, and 8th terms of another AP forms the first three terms of a geometric progression (GP).If the common difference of the AP is 3. Find
(i) The first term of GP (4mks)
(ii) The sum of the first 9 terms of the GP to 4 s.f. (2mks)
10 marks