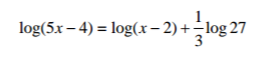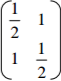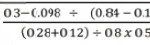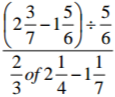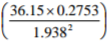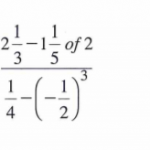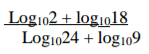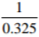KNEC KCSE Mathematics Paper 2 – 2014 Homa-Bay Mock
2014 Homa-Bay Mock
Mathematics Paper 2
SECTION I (50 Marks)
Answer All Questions from this section in the spaces provided
Evaluate using logarithms
4 marks
A business lady bought 180 mangoes at Shs.60 for every five mangoes. She sold some of them at
Shs.30 for every three and 33 1/3 % the rest at Sh.30 for every four. If she made a 33 1/3 % loss,
calculate the number of mangoes sold at Shs.30 for every four.
3 marks
Write an equation of a circle that has a diameter whose end points are at (2,7) and (-6, 15) in the
form x2+y2+ax+by+c=0 where a,b and c are integers.
3 marks
Miss Jaber bought a motor cycle at Shs.160,000. The depreciation rate was 6% per annum
determined semi annually. How long will it take the motor cycle to be valued at a quarter of its
original cost
3 marks
Given that 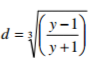
3 marks
An arithmetic progression of 41 terms in such that the sum of the first five terms in 560 and sum of
the last five terms is -250. Find the first term.
3 marks
(a) Expand and simplify the binomial expression (2x-y)5(1mk)
(b) Use the first four terms of the expansion above to approximate the value of (3.8)5(2mks)
3 marks
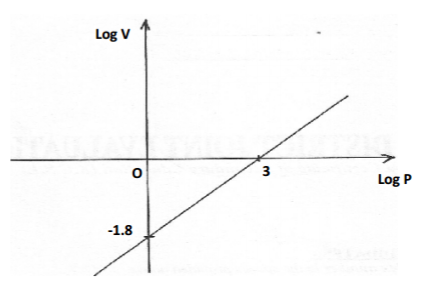
The graph below is part of the straight line graph obtained from the initial equation V=apn
(a) Write down the equation of the straight line in the form y=mx+c (1mk)
(b) Use the graph to calculate the values of a and n (2mks)
3 marks
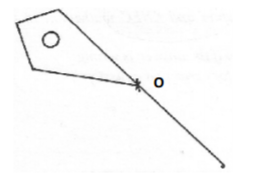
In the figure below kite ABCD represents a part of a county government logo. The logo has
symmetry order 4 about O. Complete the figure to show the logo.
2 marks
The velocity V of a body moving in a straight line at any time t is given by V=3t-2. Its distance S at
time t=0 is equal to 4m. Calculate the distance when t=4 seconds.
3 marks
The sides of a triangle were measured and recorded as 4cm, 6.2cm and 9.50cm. Calculate the
percentage error in its perimeter, correct to 2 decimal places.
3 marks
The size of an interior angle of a regular polygon is x2 while its exterior angle is 3x. Find the number
of sides of the polygon.
4 marks
Without using logarithms table, solve the equation.
3 marks
A rectangle ABCD is such that AB=6cm, and BC=5cm. A variable point P moves inside the
rectangle such that AP PB and AP >2.5cm. Show the region where P lies.
3 marks
Without using a calculator or mathematical table, express 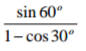
3 marks
An angles of 0.9 radians at the centre of the circle subtends an arc of length 28.8cm. Find
(a) The radius of the circle (2mks)
(b) The area of the sector enclosed by the arc and radii (2mks)
4 marks
SECTION II (50 Marks)
Answer any five questions from the section in the spaces provided .
Mr. Alvin George, a civil servant gets a monthly salary of Shs. 48,000. He lives in a government house where he pays nominal rent of Shs.2500. Besides this he gets an automatic house allowance of Shs.12000 and medical allowance of shs.8000 per month. He gets a gamily relief of sh.1065 per month. The rates of income tax are shown below
| Income tax in K£ per month | rates in shs. Per K£ |
| 1-400 | 10% |
| 401-1200 | 15% |
| 1201-2400 | 25% |
| 2401-3600 | 35% |
| 3601 and above | 45% |
Calculate:
(a) His taxable income per month in Kenya pounds (2mks)
(b) Net tax per month in Kshs. (6mks)
(c) Net salary (2mks)
10 marks
The vertices of a rectangle are A(-1,-1) B(-4,-1) C)-4,-3) and D(-1,-3)
(a) On the grid provided, draw the rectangle and its image AlBlClD under a transformation whose
matrix is 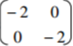
(b) A2,B2,C2,D2 is the image of A1,B1,C1,D1 under a transformation matrix
(i) Determine the co-ordinates of A2B2C2D2 (2mks)
(ii) On the same grid draw the quadrilateral A2B2C2D2 (1mk)
(c) Find the area of A2B2C2D2 (3mks)
10 marks
A solution whose volume is 120 litres is made up of 35% water and the rest alcohol. When y litres of
alcohol is added the percentage of water drops to 15%
(a) Find the value of y (4mks)
(b) The new solution is diluted further by addition of seventy litres of water. Calculate the
percentage of alcohol in the resulting solution (2mks)
(c) A blend is made by mixing 10 litres of the solution in (b) above with 20 liters of the
original solution. Calculate in the simplest form, the ratio of water to that of alcohol in the
blend (4mks)
10 marks
A passenger plane takes off from airport A(60oN,5oE) and flies directly to another airport
B(60oN,17oE) and then flies due North for 60o nautical miles (nm) another airport C.
(a) Find the position of airport C (3mks)
(b) Find the distance between airport A and B in nautical miles (3mks)
(c) If the plane at an average speed of 300knots, find total flight time (2mks)
(d)Given that the plane left air port A at 9.20am. Find the local time of arrival at airport C(2mks)
10 marks
In a certain country, the probability of a school A topping in county exams is 1/3. If it tops the
probability of it topping in KCSE is 5/7 otherwise the probability of it topping in KCSE is 2/9. If the
school tops in KCSE the probability of its appearing in the newspaper is 2/5, otherwise the
probability of its appearing in newspaper is 4/11.
(a) Draw a tree diagram to represent the above information (2mks)
(b) Use the tree diagram to find the probability that:
(i) The school tops in the two exams and appears in the newspaper (2mks)
(ii) The school did not appear in the newspaper (2mks)
(iii) The school topped in atleast one exam and did not appear in the newspaper (2mks)
(iv) The school appeared in the newspaper (2mks)
10 marks
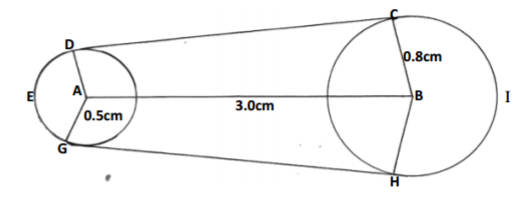
The diagram below shows a design model of a race course drawn to scale of 1:5000,000. It consists of two circles centre A and B radii 0.5cm and 0.8cm respectively and the distance between their centres is 3.0cm
Calculate in km:
(i) The length of leg CD (2mks)
(ii) The length of the leg DEG 
(iii) The length of the leg HIC (pie=3.142)(2mks)
(iv) During a race, the course is manned by race officials placed 500m apart and each is paid
Kshs.2300/= per day. How much is needed to pay race officials for one day event (4mks)
10 marks
A relief organization has to transport atleast 80 people and atleast 18 tonnes of supplies to a site.
There are two types of vehicles available type A and B. type A can carry 900kg of supplies and 6
people while type B can carry 1350kg of supplies and 5 people. There are at most 12 vehicles of each
type available. By putting X to represent the number of vehicles of type A and y to represent the
number of vehicles of type B
(a) Write down all the four inequalities to represent the above information (4mks)
(b) On the grid provided, draw all the inequalities in (a) above (4mks)

10 marks
Given that y=2x0+ cos ½ x0, complete the table below for the missing values of y, correct to 1
decimal place
(b) On the grid provide below, draw the graph of y=sin 2x0+cos ½ x0 for 0 x 360o Take the scale 1cm for 30o on the x-axis. 2 cm for 0.5 units on the y –axis. (4mks)
(c) Use the graph to estimate
(i) The minimum value of y
(ii) The value of X for which ½ sin 2x + ½ cos ½ x0.25
10 marks