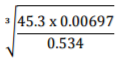KNEC KCSE Mathematics Paper 2 Question Paper / 2016 KCSE MOKASA Joint Examination
2016 KCSE MOKASA Joint Examination
Mathematics Paper 2
SECTION A (50 Marks)
Use logarithm tables to evaluate:
4 marks
The external and internal diameters of a cement pipe are 20cm and 14cm respectively.
Calculate the volume of cement required to prepare 1.4m long. Give your answer in cm3.
3 marks
Make h the subject of the formula .
3 marks
Solve for x in the equation 2 Sin2 x – 1 = Cos2x + sin for 0o < x < 390o
3 marks
The points A(-4,1) and B(-2,5) are the end points of a diameter of a circle. Determine the
coordinates of the centre of the circle, hence calculate the equation in the form:
x2 + y2 = 2ax – 2by + c + d —- = 0
3 marks
Solve the quadratic equation 3x2 – 4x = 2
3 marks
Evaluate by rationalizing the denominator and leaving your answer in surd form.
√8/1 + Cos45o
3 marks
Expand (2 + 3x)6 up to the term x2. Hence use your expansion to estimate (2.09)6
3 marks
Two quantities M and N are such that M varies partly as N and partly as the square of N.
Determine the relationship between M and N given that when M is 1050, N = 10 and when
M = 2200, N = 20.
3 marks
A dealer has two types of grades of tea, A and B. Grade A costs sh 140 per kg. Grade B costs
sh. 160 per kg. If the dealer mixes A and B in the ratio 3:5 to make a brand of tea which he
sells at sh. 180 per kg, calculate the percentage profit that he makes.
3 marks
Onyango bought a refrigerator whose cash price is sh. 84,000 on hire purchase. He made a
cash deposit of sh. 20,000 and the 15 monthly instalments of shs. 6,000. Calculate the rate of
interest per month.
3 marks
Given that OA = 2i + 5k and OB = 71 – 5j. A point T is on AB such that 2AT = 3TB.
Calculate the magnitude of OT to 4 significant figures.
3 marks
Find the sum of A.P having 15 terms, the fourth term being -3.2 and the eight term 8.4
3 marks
Use matrix methods to solve the following simultaneous equation
4 marks
The volumes of two similar cylinders are 3240cm2 and 960cm3. If the surface area of the
larger cylinder was 792cm2. find the surface area of the smaller cylinder.
3 marks
Estimate the area bounded by the curve y = ½ x2 + 1, x = 0, x = 3 and the x-axis using the
mid-ordinate rule. Use three strips.
3 marks
SECTION B (50 Marks)
The angle of elevation of the top of a flag post from a point P on a level ground is 20o. The
angle of elevation of the top of the flag post from another point Q nearer to the flag post and
110m from P is 32o. Q is between P and the flag post.
a) Draw a sketch diagram to show the above arrangement (2 marks)
b) calculate correct to 2 d.p
(i) The distance from the point Q to the top of the flag post (5 marks)
(ii) The length of the rope tied from the top of the flag post to the point P on the
ground, if 0.5m of the rope is used fro tying the knots. (3 marks)
10 marks
The diagram below shows a right pyramid with a square base ABCD and vertex V. O is the
centre of the base. AB = 14m, VA = 20m and N is the midpoint of BC.
Find;
a) The lengths of BO, VO and VN (3 marks)
b) The angle between VO and plane VBC (3 marks)
c) The angle between VB and base ABCD (2 marks)
d) The angle between VDC and VBC (2 marks)
10 marks
A number of students were asked to cut 30cm lengths of binding wire without measuring.
Later 100 pieces area collected and measured correct to the nearest 0.1 cm the data below
was collected.
| Length l (cm) |
28.0 – 28.4 |
28.5 – 28.9 |
29.0 – 29.4 |
29.5 – 29.9 |
30.0 – 30.4 |
30.5 – 30.9 |
31.0 – 31.4 |
31.5 – 31.9 |
| Frequency | 5 | 8 | 30 | x | 10 | 20 | 20 | 4 |
a) i) Calculate the value of x (1 mark)
ii) State the modal class (1 mark)
b) Using 29.7 as a working mean calculate;
i) the mean (4 marks)
ii) the standard deviation (4 marks)
10 marks
A transformation represented by matrix 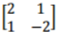
a) Draw ABCD and its image A1B1C1D1 (4 marks)
b) A transformation represented by 
c) Determine the matrix of a single transformation that maps A11B11C11D11 onto ABCD (3 marks)
10 marks
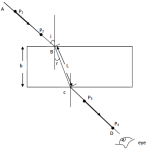
In the figure K, L, M and N are points on the circumference of a circle centre O. The points
K, O, M and P lie on a straight line.
PT is a tangent to the circle at N. Given that <MKN = 40o. find the values of the following
angles stating reasons.
a) <MLN (2 marks)
b) <OLN (2 marks)
c) <LNP (2 marks)
d) <MPN (2 marks)
e) <KLM (2 marks)
10 marks
The position of 3 cities P, Q and R are (15o, 20oW) (50oN, 20oW) and (50o, 60oE)
respectively.
a) Find the distance in nautical miles between:
(i) Cities p and Q (2 marks)
(ii) Cities P and R, via city Q (3 marks)
b) A plane left city P at 0250h and flew to city Q where it stopped for 3 hours then flew on
to city R, maintaining a ground speed of 900 knots throughout.
(i) The local time city R when the plane left city P (3 marks)
(ii) The local time (t the nearest minute) at city R when the plane landed at R.
(2 marks)
10 marks
The table below is for function y = x3 – 7x + 6 for the range -3 < x < 3.
| x | -3 | -2 | -1.5 | -1 | 0 | 1 | 1.5 | 2 | 3 |
| y | | | | | | | | | |
a) Complete the table above. (2 marks)
b) Draw the graph of the function y = x3 – 7x + 6 for the range -3 < x < 3 (3 marks)
c) Use the graph above to estimate the roots of the following;
(i) x3 = 7x -6 (1 mark)
(ii) –x3 + 8x – 2 = 0 (2 marks)
d) By drawing a tangent, estimate the gradient of the curve y=x3 – 7x + 6 at x = -2 (2 marks)
10 marks
a) The acceleration of a particle t seconds after passing a fixed point P is given by a = 3t – 3.
Given that the velocity of the particle when t = 2 is 5 m/s, find;
(i) Its velocity when t = 4 seconds (3 marks)
(ii) Its displacement at this time (3 marks)
(iii) find the exact area bounded by the graph x = 9y – y3 and the y-axis(4 marks)
10 marks