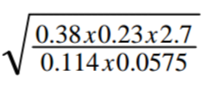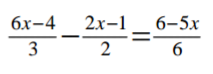KCSE Mathematics Paper 1 – 2014 EKSIKA Joint Evaluation Test
2014 EKSIKA Joint Evaluation Test
Mathematics Paper 1
SECTION I (50 Marks)
Answer all questions in this section.
Without using tables or calculators, evaluate.
3 marks
Without using a calculator or tables, find the value of y given that y = (a+b) (x – c)2 and a = 5 , b =6 , x = -3 and c = 2.
3 marks
Solve the following inequalities and represent the solution on a single number line.
3 marks
Use the reciprocal, square and square-root tables to evaluate to 4 significant figures the expression.
4 marks
5 A Kenyan bank buys and sells foreign currencies at the exchange rates shown below.
| Currency | BUYING (KSHS) | SELLING (KSHS) |
| 1Euro | 147.56 | 148.00 |
| 1U.S Dollar | 74.22 | 74.50 |
An American arrived in Kenya with 20,000 Euros. He converted all the Euros into Kenyan Shillings at the bank. He spent Kshs.2,510,200 while in Kenya and converted the remaining Kenya shillings into U.S Dollars at the bank. Find the amount in dollars that he received.
3 marks
Determine the quartile deviation of the following data 4,9,5,4,7,6,2,1,6,7,8,3.
3 marks
Translation Q is represented by the column vector 

3 marks
Find the equation of the perpendicular line that passes through the mid – point X of C( – 7 , 8) and D ( 3 , – 8)
4 marks
Mbom paid Kshs.160 for a blouse after getting a discount of 20%.The vendor made a profit of 30% on the sale of this blouse. What percentage profit would the vendor have made if no discount was allowed?
3 marks
The base of a triangle is 3cm longer than its height. Given that the area of the triangle
is 35cm2, determine the height of the triangle.
3 marks
Solve for X in the equation.
2 marks
The figure below shows a circle centre O. Chord AB subtends 30o at the centre. If the area of the minor segment is 5.25cm2, find the radius of the circle.
3 marks
A certain two–digit number is equivalent to five times the sum of the digits. It is found to be 9 less than the number formed when the digits are interchanged. Find the number.
3 marks
The surface area of two similar bottles are 12cm2 and 108cm2 respectively. If larger one has a volume of 810cm3.Find the volume of the smaller one.
3 marks
The exterior angle of a regular polygon is equal to one–third of the interior angle.
Calculate the number of sides of the polygon and give its name.
3 marks
King’oo spends one-third of his salary on food, one–quarter on rent, three–fifth of the remainder on transport and saves the rest.If he spends Kshs.1800 on transport, find how much money he saves.
3 marks
SECTION II (50 Marks)
Choose any five questions only
John bought 3 brands of tea A , B and C.The cost price of the brands were sh.25, sh.30 and sh.45 per kilogram respectively. He mixed the brands in the ratio of 5:2:1 respectively. After selling the mixture, he made a profit of 20%.
(a) How much profit did he make per kilogram of the mixture. (4mks)
(b) After one year, the cost price of each brand was increased by 12%.
(i) For how much did he sell one kilogram of the mixture to make 20% profit. (3mks)
(ii) What would have been his percentage profit if he sold one kilogram of the mixture at shs.40.25? (3mks)
10 marks
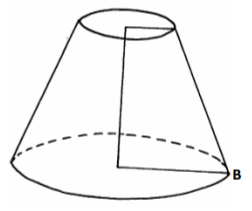
The diagram below represents a solid consisting of a hemispherical bottom and a
conical frustrum at the top. O1O2=4cm, O2B=R=4.9cm, O1A=r=2.1cm
(a) Determine the height of the chopped off cone and hence the height of the
bigger cone. (2mks)
(b) Calculate the surface area of the solid. (4mks)
(c) Calculate the volume of the solid. (4mks)
10 marks
(a) The bill for completely covering the floor of a rectangular room with carpetcosting shs.70 per square metre is shs.1960.If one side of the room is X m long; show that the length of the other side is 
(b) By leaving a uniform width of ½ m uncovered all round, shs.700 could have been saved. Use this information to form an equation in x and show that it reduces to X2 – 11x + 28 = 0. (4mks)
(c) Solve the equation and hence find the dimensions of the room. (3mks)
10 marks
The angle of elevation of the top of a flagpole from a point A on a level ground is 13o. The angle of elevation of the top of the flagpole from another point B nearer the pole and 12m from A is 30o. Find;
(a) (i) The height of the flagpole (5mks)
(ii) The distance from point B to the top of the flagpole. (2mks)
(b) 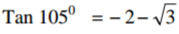
10 marks
(a) Draw the graph of the function below on the grid provided y = 2x2 – 7x – 2 for the values of -1≤X≤6 (5mks)
(b) From your graph determine the roots of the function. 2x2 – 7x – 2 = 0.(1mk)
(c) By drawing a suitable graph of function y = 2x – 7 on the same axis, solve the simultaneous equations y = 2x2 – 7x – 2 and y = 2x – 7. (4mks)
10 marks
Three people; A , B and C work together to make a certain number of tins. If person C was to work alone he will take 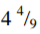
(a) Person A alone? (6mks)
(b) Person B alone? (2mks)
(c) Person A and C alone? (2mks)
10 marks
In the figure below O, is the centre of the circle. 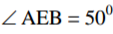
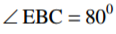
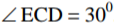
Giving reasons, calculate
10 marks
Patients who attended clinic in one week grouped by age as shown in the table below.
| X Age (years) | No. of patients |
| 0 – 5 | 14 |
| 5 – 15 | 41 |
| 15 – 25 | 59 |
| 25 – 45 | 70 |
| 45 – 75 | 15 |
(a) Estimate the mean age. (4mks)
(b) On the graph provided , draw a histogram to represent the distribution.(6mks)
10 marks