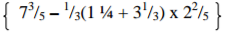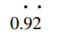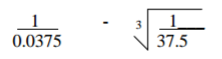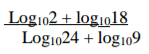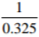KNEC KCSE Mathematics Paper 1 – 2014 Gatundu Mock
2014 Gatundu Mock
Mathematics Paper 1
SECTION 1 (50 Marks)
ANSWER ALL QUESTIONS IN THIS SECTION IN THE SPACES PROVIDED BELOW EACH QUESTION.
Using logarithms tables evaluate.
4 marks
A sum of money is divided between three people, Tom, Mary and Lucy in the ratio 5:3:1. If Mary
has sh.700 more than Lucy, calculate how much Tom has.
3 marks
Evaluate 3/8 of
3 marks
Express the following as fraction.
3 marks
In the figure below, O is the centre of the circle and OB bisects angel ABC. Given that <BAC= 40o, find <ABO.
3 marks
Solve for x in the equation below:
125(x+1)+53x=630
3 marks
Find the integral values of y of which satisfy the inequalities below.
3 marks
Use reciprocal and cube root tables to evaluate.
3 marks
The position vector of points A and B relative to the origin O are a and b respectively. Given that
a = 4i + 3j and b = i + 2j, find the modulus of the vector a + b.
3 marks
Tap A takes one hour to fill a tank with water. If tap B takes y hours to remove the same water and
both taps takes 1 ½ hours to fill the tank, find the value of y.
3 marks
Obenda weighed 120kg before he was taken ill of HIV/AIDs. After sometimes his weight decreased by
10% every week for 5 weeks. He was put on ARVs and his weight increased by 5% every week for 3
weeks. What is his weight at the end of eighth week?
4 marks
The mean age of 4 girls is 15 yeas. The first and second are aged 13 years and 18 years respectively.
The third girl is 3 years older than the first girl. Find the modal age.
2 marks
Solve the following simultaneous equations.
Log2(4y + x) = 3
Log3(4x + y) = 2
4 marks
The L.C.M of 15, 18 and a third number is 1260. Find the square of third number.
2 marks
Use the currency conversion table below to answer the questions that follow.
| CURRENCY | BUYING | SELLING |
| 1 US DOLLAR | Ksh.78.4133 | Ksh.78.4744 |
| 1 EURO | Ksh.73.4226 | Ksh.73.5295 |
An American tourist came to Kenya with US dollar 10,000. He converted all his money to Kenya
shilling and used Ksh.32,000 while he was in Kenya. The tourist converted the remainder to Euros
because he wanted to visit Germany. How much did he get (give the answer to 4 decimal places)
3 marks
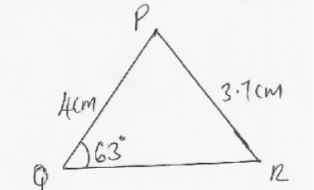
Find the length QR of the following triangle if PR=3.7cm PQ=4cm and <PQR = 63o
4 marks
SECTION II (50 Marks)
ANSWER ANY 5 QUESTION FROM THIS SECTION
Mr. Biwott operates two passenger service vehicles along Nakuru- Eldoret route. One is a 16 seater
Matatu and the other is 8-seater van. Each vehicle makes one route trip per day and the charges are ksh 250 and ksh 300 per passenger respectively (one way). The matatu uses diesel which costs ksh.48 per litre and the van uses regular petrol which costs ksh.52 per litre. The fuel consumption of the two vehicles is in the ratio of 4:3 respectively.
(a) If the matatu uses 80 litres for the round trip, determine the fuel consumption of the van for the
round trip. (2 marks)
(b) Calculate the daily collection for each vehicle. (2 marks)
(c) Determine which vehicle is more profitable (on daily basis) and by how much. (3 marks)
(d) If the price of both types of fuel goes up by 20% determine the percentage change in daily
collection. (3 marks)
10 marks
Two airports are such that B is 500km due East of A. Two planes P and Q take off from A and B
respectively and at the same time. Place P flies at 360km/h on a bearing of 030o. Plane Q flies at
240km/h on a bearing of 315o. The two planes land after 90 minutes. Using a scale of 1:10,000,000:
(a) Show the positions of the planes after 90 minutes. (7 marks)
(b) Find the distance between the planes after 90 minutes. (1 mark)
(c) Find:
(i) The bearing of plane P from plane Q after 90 minutes. (1 mark)
(ii) The bearing of plane Q from plane P after 90 minutes. (1 mark)
10 marks
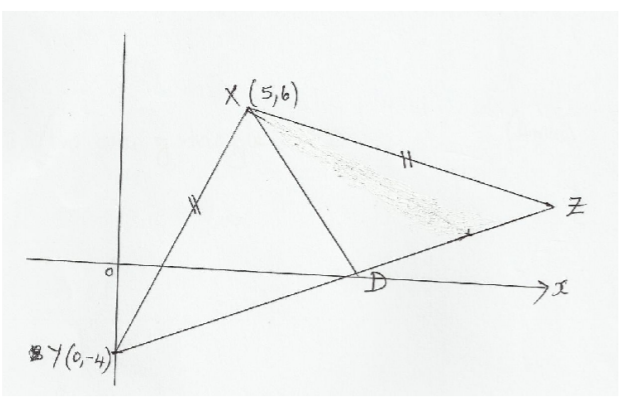
The diagram which is not drawn to scale, shows an isosceles triangle XYZ in which XY=YZ. The
coordinates of x and y are (5,6) and (0, -4) respectively.
Given that the equation of line YZ is y=3/4x – 4 and that the perpendicular from X to YZ meet YZ at D, find.
(i) The equation of XD (2 marks)
(ii) The coordinate of D (2 marks)
(iii) The coordinates of Z (2 marks)
(iv) The area of triangle XYZ (4 marks)
10 marks
(a) On the grid provided plot the points A(1, 5) B(3, 1) C(4, 4) and D(3, 3). Join these points to form quadrilateral ABCD. (2 marks)
(b) The points A1(2, 10) B1(6, 2) C1(8, 8) and D1(6, 6) are the images of A, B, C and D under a certain enlargement. On the same grid draw the image A1B1C1D1(2 marks)
(c) Use the construction method to locate the centre of enlargement and state its coordinates. (2 marks)
(d) What is the scale factor of this enlargement? (1 mark)
(e) Determine the matrix of this enlargement. (3 marks)
10 marks
Draw the graph of the given function over the given range and use it to solve the given equation.
Range -4<x <4. y = 2x2 + x – 1 hence solve (5 marks)
(a) 2x2 + 5x + 4 = 0 ( 1 mark)
(b) 2x2 + 5x + 2 = 0 (2 marks)
(c) 2x2 + 4x + 3 = 0 (2 marks)
10 marks
The figure below shows a uniform cross-section of a swimming pool which is 4m wide. The depth of
the pool increase gently from 1.5m to 3.0m.
(a) How much water in litres does it hold when full? (3 marks)
(b) Calculate total internal surface area of the pool. (5 marks)
(c) Find the angle at which the bottom of the pool inclines to the horizontal. (2 marks)
10 marks
(a) Using a ruler and a pair of compasses only construct a rhombus A B C D such that AB = 6cm and
<ABC = 135o. (4 marks)
(b) Drop a perpendicular from C to AB extended to meet AB at N. Measure BN and CN. (3 marks)
(c) Bisect <ABC and <DAB, let the two bisectors meet at M. Measure MA. (1 mark)
(d) Determine the area of triangle ABM. (2 marks)
10 marks
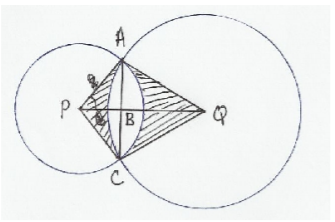
Two intersecting circles have centres P and Q as shown below. The circle centre P has radius 8cm and that of centre Q has radius 9cm.
The distance between the centres PQ = 14cm and PB:BQ = 3:4. Calculate
(i) Angles APC (2 marks)
(ii) Angle AQC (2 marks)
(iii) The area of the shaded region. (6 marks)
10 marks