KNEC KCSE Mathematics Paper 1 Question Paper / 2014 Kakamega County Mock
2014 Kakamega County Mock
Mathematics Paper 1
SECTION I (50 Marks)
ANSWER ALL QUESTIONS IN THIS SECTION IN THE SPACES PROVIDED BELOW EACH QUESTION.
Use tables of reciprocal only to evaluate 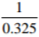
3 marks
Solve the equation 3x2+4x+2=2 giving the roots correct to two decimal places.
4 marks
The straight line through the points D (6, 3) and E (3, -2) meets the y-axis at the point F. Determine
the coordinates of F.
3 marks
Using the grid provided below, draw and shade the unwanted regions to show the region satisfied by
R given the following inequalities; y + x < 5, y + x < 1 and x + 5y > 5.
3 marks
Given that a = -2, b = -1 and c = 3, evaluate
3 marks
A key cutting factory starts cutting keys at the rate of 500 per hour. The rate of production reduces by
10% every 2 hours. Calculate the numbers of keys cut in the first 6 hours.
2 marks
Two boys and a girl shared some money .The elder boy got 4/9 of it, the younger boy got 2/5 of the
reminder and the girl got the rest. Find the percentage share of the younger boy to the girl’s share.
3 marks
Annette has some money in two denominations only. Fifty shilling notes and twenty shilling coins.
She has three times as many fifty shilling notes as twenty shilling coins. If altogether she has sh. 3400, find the number of fifty shilling notes and 20 shilling coins.
3 marks
The figure below shows a rhombus PQRS with PQ = 9cm and SPQ=60o. SXQ is a circular arc;
centre P.Calculate the area of the shaded region correct to two decimal places. ( take 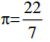
4 marks
A particle accelerates uniformly from rest and attains a maximum velocity of 30m/s after 16 seconds.
It travels at this constant velocity for the next 20 seconds before decelerating to rest after another 8
seconds. Calculate the total distance covered by the car.
3 marks
The figure below shows a right angled triangle with AB = 12cm. ED is parallel to BA, CE = 6.3cm
and ED = 8cm. Given that the area of EBAD = 31.5cm2, find the length of BC.
4 marks
Find the value of x in the equation
3 marks
Given that tan x = 2.4 , evaluate without use of tables and calculators, sin x – cos x in the form of a/b
where a and b are integers.
4 marks
The difference between the interior and exterior angles at each vertex of a regular polygon is 162o . Find the number of sides of the polygon.
2 marks
A number n is such that when it is divided by 27 and 30 or 45, the remainder is always 3. Find the
smallest value of n.
2 marks
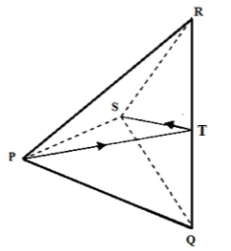
The figure below shows a regular tetrahedron PQRS of edges 4cm.
Draw its net and measure the length of the straight path of PS through the midpoint T over the edge
QR.
3 marks
SECTION II (50 Marks)
ANSWER ALL QUESTIONS IN THIS SECTION IN THE SPACES PROVIDED BELOW EACH QUESTION.
Three business partners, Bela, Joan and Trinity contributed Kshs. 112, 000, Kshs. 128, 000 and Kshs. 210, 000 respectively to start a business. They agreed to share their profits as follows:
30% to be shared equally
30% to be shared in the ratio of their contributions
40% to be retained for the running of the business.
If at the end of the year, the business realised a profit of Kshs. 1. 35million
Calculate:
(a) the amount of money retained for running the business at the end of the year. (1mark)
(b) the difference between the amounts received by Trinity and Bela. (6marks)
(c) Express Joan’s share as percentage of the total amount of money shared between the three
partners. (3 marks)
10 marks
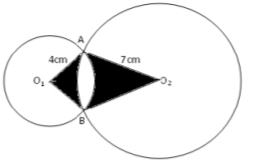
In the figure below, O1 and O2 are the centres of the circles whose radii are 4 cm and 7 cm
respectively. The circles intersect at A and B and angle AO1O2 = 60˚
Find by calculation; take π = 3.142
(a) The angle AO2O1 (1 marks
(b) The area of the quadrilateral AO1BO2 (4 marks)
(c) The shaded area (5 marks)
10 marks
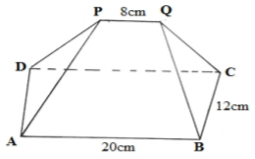
The figure below shows a plan of a roof with a rectangular base ABCD. AB = 20cm and BC = 12cm.
the ridge PQ = 8cm and is centrally placed. The faces ADP and BCQ are equilateral triangles. N is the
midpoint of AD.
Calculate:
(a) The length of PN (2 marks)
(b) The altitude of P above the base. (3 marks)
(c) The angle between the planes ABQP and ABCD. (2 marks)
(d) The obtuse angle between the lines PQ and DB (3 marks)
10 marks
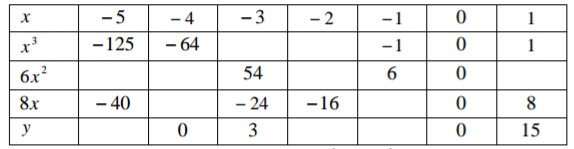
Complete the table below for the function y = x3 + 6 x2 + 8x for -5 < x < 1 (3 marks )
(a) Draw the graph of the function y = x3 + 6 x2 + 8x for -5 <x < 1 (3 marks)
(Use a scale of 1cm to represent 1 unit on the x axis. 1 cm to represent 5 units on the y-axis)
(b) Hence use your graph to estimate the roots of the equation x3 + 5x2 + 4x = -x2 – 3x – 1 (4 marks)
10 marks
Three islands P, Q, R and S are on at ocean such that island Q is 400kmon a bearing of 030o from island P. Island R is 520kmand on a bearing of 1200 from island Q. A port S is sighted 750km due south of island Q.
(a) Taking a scale of 1cm to represent 100km, give a scale drawing showing the relative positions of
P, Q, R and S. (4 marks)
Use the scale drawing to
(b) Find the bearing of:
(i) Island R from island P (1 mark)
(ii) Port S from island R (1 mark)
(c) Find the distance between island P and R (2 marks)
(d) A warship T is such that it is equidistant from the islands P, S and R. By construction locate the
position of T (2 marks)
10 marks
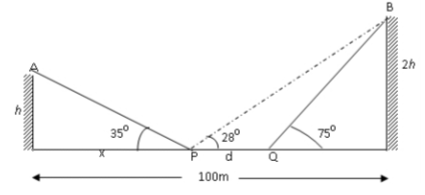
Two vertical columns A and B of height h and 2h respectively stand on level ground and are 100m
apart. Two points P and Q are d metres apart, the elevation of the top of A and B from point P are 35o
and 28o respectively and the elevation of top of B from point Q is 75o.
Calculate
(a) The vertical heights of the two columns in metres (7 marks)
(b) The distance PQ in metres (3 marks)
10 marks
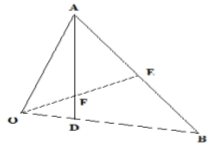
In the figure below, E is the midpoint of AB, OD : DB = 2 : 3 and F is the point of intersection of OE
and AD
Given that OA = a and OB = b, (a) Express in terms of a and b
(i) AD (1 mark)
(ii) OE (2 marks)
(b) Given further that AF = sAD and OF = tOE, find the values of s and t (5 marks)
(c) Show that E, F and O are collinear (2 marks)
10 marks
A swimming pool is 20m by 12m and it slopes gently from a depth of 1m at the shallow end to a depth
of 3m at the deep end.
(a) Calculate the volume of water in the swimming pool (in m3) when it is full. (3marks)
(b) If the swimming pool is to be drained by a pump which removes water at the rate of 2.5m3 per
minute, how long will it take this pump to drain the swimming pool if it was full? (3marks)
(c) If the sides of the swimming pool and its floor are to be covered with square tiles of side 20cm,
find to the nearest 100 the number of tiles required. (4marks)
10 marks
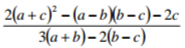
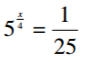
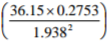


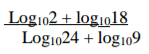
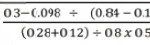

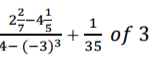
I good website indeed!
Nice Questions