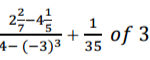KNEC KCSE Mathematics Paper 1 Question Paper / 2015 KCSE Kajiado County Joint Examination
2015 KCSE Kajiado County Joint Examination
Mathematics Paper 1
SECTION I: (50 Marks)
Answer all the questions in this section
Without using mathematical tables or calculators evaluate:
√1296
6+ −18 ÷ +(5− −3)
3 marks
Use reciprocal and square tables to evaluate to 4 significant figures the expression: (3 Marks)
1
24.56 + 4.3462
3 marks
Points A(2,7) and B(-4,3) are points on a straight line. Find the equation of the perpendicular bisector of the line AB.
4 marks
Using a ruler and a pair of compasses only, construct a trapezium ABCD with AB parallel to DC. AB = 10cm, BC = 5cm, CD = 4cm and angle ABC = 450. Drop a perpendicular from C to meet AB to O. Measure AD and the altitude of the trapezium.
4 marks
Simplify completely:
(𝑥𝑥−3𝑦𝑦)2−(𝑥𝑥+3𝑦𝑦)2
4𝑥𝑥𝑥𝑥
3 marks
A mobile phone seller gets a commission of Shs. 250 on every mobile phone that he sells. In a given month, he got 33,000 shillings.
(a) How many phones did he sell that month. (1 Mark)
(b) If this commission is 2%. What is the sale price of each mobile phone? (2 Marks)
3 marks
Find the equation of the normal to the curve y = x2 + 3x at the point P where x = 1.
3 marks
A test is conducted for the purpose of employing a suitable typist with the following results.
Speed words per minute 30-34 35-39 40-44 45-49 50-54 55-59 60-64
No. of candidates 2 4 8 10 12 3 1
Calculate the mean typing speed.
3 marks
PQRS is a cyclic quadrilateral and O is the centre of the circle. ∠QOS = 1500
While giving reasons find:
(a) ∠QPS (2 Marks)
(b) ∠QRS (1Mark)
3 marks
The angle subtended by the major arc at the centre of the circle O is twice the angle subtended by the minor arc at the centre. If the radius of the circle is 3.5cm, find the length of the minor arc. (Take 𝜋𝜋 = 22
7 )
3 marks
The image of P(0,2) under an enlargement with the factor 3 is P1(4,6). Find the centre of enlargement.
3 marks
Given that x is an acute angle and sin x = 2√5 √5 , find without using tables or calculator tan (90 – x)0 leaving your answer in its simplest form.
3 marks
A regular polygon with 3x sides has interior angle 400 greater than the one with x sides. What is x?
3 marks
(a) Solve the following inequalities and hence illustrate your solution on a number line. (2 Marks)
x – 12 ≤ 4x – 15 < 13
(b) List the integral values that satisfy the combined inequality above. (1Mark)
3 marks
Determine the values of m for which the matrix below has no inverse (3 Marks)
�
1
3 𝑚𝑚 𝑚𝑚2
3 1
�
3 marks
A quantity y is partly constant and partly varies as x3. If y = 7 when x = 10 and y = 12 3
80 when x = 20, write an equation connecting y and x.
3 marks
SECTION II: (50 Marks)
Answer only five questions in this section.
The figure below a frustum of a solid cone of base radius 48cm and top radius 16cm. The height of the frustum is 21cm. (Take 𝜋𝜋 = 22 7 ) calculate:
(a) The height of the solid cone. (2 Marks)
(b) The volume of the solid frustum. (3 Marks)
(c) The total surface area of the frustum. (5 Marks)
10 marks
The following are masses of 25 people taken in a clinic.
20 35 29 45 60
66 56 29 48 37
59 64 24 28 32
35 45 48 52 55
54 55 36 39 35
(a) Using a class width of 8 and starting with the lowest mass of the people. Make a frequency distribution table for
the data. (3 Marks)
(b) Calculate the median mass of the people. (3 Marks)
(c) On the grid provided, draw a histogram to represent the information. (4 Marks)
10 marks
In triangle OAB, OA = a, OB = b and P lies on AB such that AP:PB = 3 : 5.
(a) In terms of a and b the vectors.
(i) AB (1Mark)
(ii) AP (2 Marks)
(iii) BP (2 Marks)
(iv) OP (2 Marks)
(b) Point Q is on OP such that AQ = –
5
8
a + 9
40
b (3 Marks)
Find the ratio OQ:QP
10 marks
(a) Draw the curve y = x2, for 0 < x < 3.
Take 2cm to represent 1 unit x-axis and 1cm to represent 1 unit on the y-axis. (5 Marks)
(b) Use the graph to estimate the area bounded by the curve y = x2, the x-axis and the lines x = 0 and x = 3 using
trapezia. (correct 3 d.p) (3 Marks)
(c) Given the actual areas as 9cm2 calculate the percentage error. (2 Marks)
10 marks
Town A and B are 24km apart. Susan leaves town A at 10.00 a.m and cycles to town B at a steady speed if 12km/h. She rests for exactly one hour and then runs back to town A at 8km/h. Jane leaves town B at 11.45 a.m and rides straight to town A, where reaches 5 minutes after Susan.
(a) At what time did Susan leave town B. (2 Marks)
(b) At what time did Jane reach town A. (3 Marks)
(c) How fast did Jane ride? (2 Marks)
(d) At what time did Susan overtake Jane? (3 Marks)
10 marks
In a bicycle rally, cyclists are to follow routes VWXY. W is 250km from V on a bearing of N750E from V. X is on a bearing of S700E from V and 275km from W. Y is 300km on a bearing of N400E from X. Using a scale of 1cm to represent 50km.
(a) Draw a diagram to show the relative positions of VWXY. (4 Marks)
(b) Determine the distance in km
(i) VX (1 Mark)
(ii) XY (1 Mark)
(iii) WY (1 Mark)
(c) (i) Determine the compass bearing of W from X (1 Mark )
(ii) The compass bearing of Y from W (1 Mark)
(iii) The compass bearing of X from Y (1 Mark)
10 marks
AMREF Kenya decided to buy y bicycles for a total cost of 72,000 shillings. The seller agreed to offer a discount of 200 shillings per bicycle. AMFREF Kenya was able to buy 4 extra bicycles for the same amount of money.
(a) Write an expression in terms of y for the:
(i) original price of each bicycle (1 Mark)
(ii) price of each bicycle after the discount (1 Mark)
(b) Form an equation in y and hence determine the number of bicycles AMREF Kenya bought. (5 Marks)
(c) Calculate the discount offered to AMREF Kenya as percentage. (3 Marks)
10 marks
Given that the curve y = x3 – 3×2 find:
(a) The coordinate of the stationary points of the curve. (4 Marks)
(b) Sketch the curve y = x3 – 3×2 (6 Marks)
10 marks