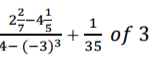KNEC KCSE Mathematics Paper 2 Question Paper / 2015 KCSE Meru South Form 4 Joint Examination
2015 KCSE Meru South Form 4 Joint Examination
Mathematics Paper 2
SECTION I (50 Marks)
Answer ALL questions in this section
The seventh term of an arithmetic progression is 15 while twice the third is 94. Calculate the first term and the common difference of the progression.
3 marks
The sides of a triangle were measured to 1dp as 6.4cm, 7.3cm and 8.2cm respectively. Calculate the percentage error in its perimeter.
3 marks
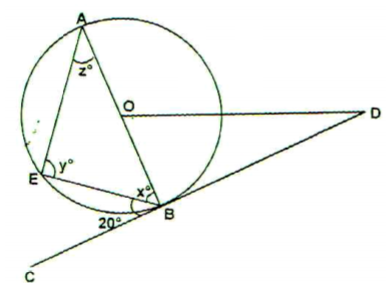
In the figure below AB is the diameter, CD is a tangent to the circle at B and angle CBE is 20o.
Calculate the angles labelled x, y and z.
3 marks
Simplify the fraction.
3 marks
The table below shows masses of marbles in a certain lab.
| Mass(g) | Number of marbles |
| 20.0-20.4 20.5-20-9 21.0-21.4 21.5-21.9 22.0 – 22.4 22.5 – 22.9 |
5 7 16 10 14 13 |
Estimate the median using calculation.
4 marks
Given that Sin θ = 5/13, determine the value of tan (90 – θ) without using a calculator or mathematical tables.
2 marks
Points P(2,3) and Q (4,5) are mapped into P1 (12,14) and Q1 (22,24) respectively by a transformation matrix T. Find the matrix T.
3 marks
Expand and simplify (2 – y)5 and use the first four terms to find the approximate value of (1.8)5 to 2 decimal places.
4 marks
AB is a diameter of a circle. Given that the coordinates of A and B are (-2,2) and (-2,6) respectively, find the equation of the circle in the form ax2 + by2 + cx + dy + e = 0.
4 marks
Solve for x in the equation.
2Log10x + Log105 = 1 + 2Log104.
3 marks
Given that 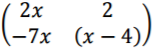
3 marks
A fire engine left the fire station at 9.15 a.m and travelled with an average speed of 64km/h. At 10.10 a.m, an ambulance left the fire station and caught up with fire engine at 11.40 am. Find the average speed of ambulance to the nearest whole number.
3 marks
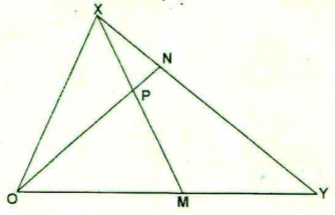
Find the length NX in the figure below that PQ = 9cm, PX = 12cm and MX = 15cm.
3 marks
In August 2014, a tourist visited Mombasa with 240 sterling pounds which she changed to Kenya Shillings at the rate of KSh. 112.00 per sterling pound. She spent KSh. 1000.00 on accommodation and a half of what remained on entertainment. The balance she converted to Sterling pounds at the rate of KSh. 113.50 per pound. How many Sterling pounds did she have left? (4 Marks)
4 marks
Give that a = 6i, b = 5i – 3j and c = 3i + j, find scalars h and k such that ha + kb = c
3 marks
SECTION II (50 Marks)
Answer only FIVE questions from this section.
(a) The nth term of a series is given by 6 – 4n.
(i) Write down the first four terms of the series. (2 Marks)
(ii) Find the sum of the first 16 terms of the series. (3 Marks)
(iii) Find the 25th term. (3 Marks)
(b) A colony of bees was found to have 100 bees at the beginning. Thereafter, the number doubled every two days. How many bees will be in the colony after 14 days? (3 Marks)
10 marks
Weather records indicate that the probability of rain falling in Chuka town in March, July and September are 9/10, 4/10 and 1/20 respectively. Calculate the probability that in a certain year:
(i) There will no rain in March, July and Sepemmber. (3 Marks)
(ii) There will be rain in March, July and September. (2 Marks)
(iii) There will be rain in at least 2 of the 3 months i.e. March, July and September. (3 Marks)
(iv) There will be rain in at most 2 of the 3 months i.e. March, July and September. (2 Marks)
10 marks
(a) In a certain year income tax was charged at the rates shown below.
| Income (K£p.a) | Rate of tax KSh. per K£ |
| 1-5808 5809-11280 11281-16752 16753 – 22224 Above 2224 |
2 3 4 5 6 |
Mrs. Munene earns a basic salary of KSh. 15000.00, a house allowance of KSh. 8,000.00 and a commuter allowance of KSh. 2,000.00 per month. She pays a health insurance scheme at Sh. 320 per month and she is entitled to a personal relief of Sh. 1156.00 per month.
Determine
(i) Her annual taxable income in K£ (2 Marks)
(ii) The income tax she pays per year after relief. (4 Marks)
(b) A taxi businessman borrows Sh. 650,000.00 from a bank to buy a taxi valued at the same amount.
The bank charges interest at 24% p.a. compounded quarterly. Calculate the compound interest paid to the bank after 1½ years rounded to the nearest shilling. (4 Marks)
10 marks
In the diagram below OX = x and OY = y, M and N are points on OY and XY respectively where OM = 1/3 OY and XN =2/5 XY. Lines XM and ON interest at P such that OP = 5/9ON.
(a) Express in terms of vector x and y.
(i) XY (1 Mark)
(ii) ON (2 Marks)
(iii) XM (1 Mark)
(b) Express XP and PM in terms of x and y (5 Marks)
(c) State the ratio XP:PM (1 Mark )
10 marks
(a) Complete the table below by filling the blank spaces.
(b) On the grid provided draw on the same axis the graph of y = 3Cos 2x and y = 2 Sin (x + 30)o for 0o≤x≤180o. Use a scale 1cm to represent 1500 on the x-axis and 2cm to represent 1 unit on the y – axis.
(4 Marks)
(c) Use your graph to
(i) Solve for x when 2Sin (x+30)o – 3Cos 2xo = 0 (2 Marks)
(ii) Estimate the range of x when 2Sin (x+30)o ≥ 3Cos2x giving your answer to the nearest degree. (1 Mark)
10 marks
Two variables P and T are related by the formula P = yTx where x and y are constants. The table below gives some values of the independent variable T and the corresponding values of the dependent variable P.
| T | 2 | 3 | 4 | 5 | 7 |
| P | 44.9 | 118.7 | 236.8 | 404.5 | 907 |
(a) Complete the table below correct to 2 decimal places for log T and log P. (2 Marks)
(b) Given that the two variables P and T satisfy the linear equation in the form of Log = p log y + xlogT, plot log p against T in the grid provided. Hence draw a line of best fit.
(Use a scale of 2cm:0.1 units in the axis and 2cm : 0.5 units in the y axis)
(c) Use your linear graph to obtain, correct to 1 d.p
(i) Constants x and y (3 Marks)
(ii) P when T = 6 (2 Marks)
10 marks
(a) Complete the table given below for y = x3 – 4x2 + x + 6 for -2< x < 4. (3 Marks)
(b) On the grid provided draw the graph of y = x3 – 4x2 + x + 6 for -2< x <4. Use of a scale of 2cm to represent 1 unit on the x-axis and 1cm to represent 2 units on the y axis. (3 Marks)
(c) Use your graph to solve the equation x3 – 4x2 + x = 6 (1 Mark)
(d) By drawing a suitable straight the line estimate the roots of the equation. (3 Marks)
10 marks
(a) X is directly proportional to the square y. What is the percentage change in x if y increases by 25%. (5 Marks)
(b) The mass of a solid metal ball varies jointly as a specific variable S and the cube of its diameter.
When the diameter is 6cm S = 7.5 and the mass is 850g. Find the mass of the ball of S = 10.5 and diameter 8cm giving your answer to the nearest whole number. (5 Marks)
10 marks