KNEC KCSE Mathematics Paper 2 Question Paper / 2016 KASSU JET JOINT EXAMINATION
2016 KASSU JET JOINT EXAMINATION
Mathematics Paper 2
Use logarithm tables to evaluate;
3 marks
The middle digit of a number between 100 and 1000 is zero, and the sum of the other digits is 11.
If the digits are reversed the number so formed exceeds the original by 495. Find the number.
3 marks
Without using mathematical tables or a calculator evaluate
Leaving the answer as a decimal
3 marks
Expand (0.07)5 using binomial theorem giving your answer to four significant figures
3 marks
Solve for θ in the equation Sin (3θ + 120o) = √3/2 in the range 0 ≤θ≤ 180o.
3 marks
Rationalize the denominator leaving your answer in the form a + b√𝒄𝒄 wherea, b and c are
constants
3 marks
A farmer bought a machine at a current price of Ksh 224,000. If the depreciation rate is 5% in
every 3 months. Calculate the sum of its value in 3 years ago and 3 years’ time.
3 marks
Without using logarithm table or calculators, find the value of p in the equation.
Log n3 + log 4n = 10 log2 – log (28� )
3 marks
Using mid-ordinates rules, estimate the area under the curve y= ½ x2 -2, using six strips between
x=2 and x=8 and x-axis
3 marks
(a) Using a pair of compass and a ruler only Construct a triangle PQR in which PQ=QR=4cm
and angle QPR= 30o. (2mks)
(b) A point T is always on the same side of PQ as R and angle PRQ=angle PTQ. Construct the
locus of T and describe it. (2mks)
4 marks
R is partly constant and partly varies as the square of q. when R = 5, q = q and R = 21, when q =
3. Find the value of R when q = 5.
3 marks
The first, the third and the seventh term of an increasing arithmetic progression are three
consecutive terms of a geometric progression. If the first term of the arithmetic progression is 10, find the common difference of the arithmetic progression.
3 marks
The equation of a circle is x2 – 8x + y2 + 12y + 16 = 0
Determine the coordinates of the Centre of the circle and its radius.
3 marks
In the diagram above CD is a tangent to the circle at C. AC and FD intersect at B. FED is a
straight line. Given that CD = 10 cm, AB = 2 cm AC = 8 cm, FB = 3 cm. Find the length ED.
4 marks
The cost of 2 brands of coffee A and B per kilogram are 59.40 and Sh.72 respectively. The two
brands are mixed in the ratio x:y and sold at a profit of 20% above the cost. If the selling price per
kilogram mixture is Ksh.72. find the value of x and y.
3 marks
Evaluate
3 marks
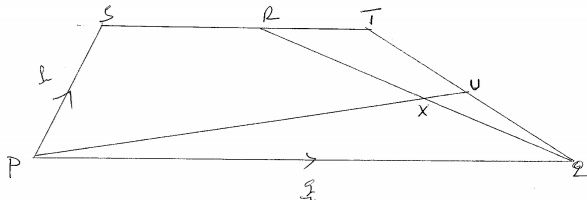
In the trapezium shown below𝑷
QT. PU and QR intersect at X. PX = hPU and QX = kQR
Given that PQ = q and PS = p
(a) Express QR in terms of P and q (1mk)
(b) Express PX in terms of P, q and h. (2mks)
(c) Express PX in terms of P, q and k. (3mks)
(d) Hence; obtains the values of h ad k. (3mks)
(e) Determine the ratio in which X divides QR. (1mk)
10 marks
The table below shows the distribution of marks of 40 candidates in a test
| Marks | 1-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
| Frequency | 2 | 2 | 3 | x | 12 | 5 | 2 | 3 | 1 | 1 |
(a)(i) Find the value of x (1mk)
(ii) State the modal class (1mk)
(iii) Calculate the median (4mks)
(iv) Calculate the mean. (4marks)
10 marks
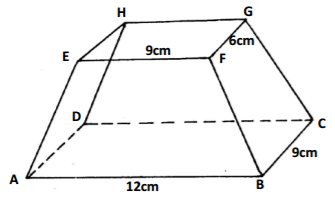
The figure below is a frustum of a rectangular pyramid with AB=12CM, EF=8CM,BC=9CM and
height of 6 CM
Calculate:
a) the full height of the pyramid 2 marks
b) angle that the plane ABFE makes with the base ABCD 2marks
c) angle that AG makes with the base ABCD 3marks
d) angle that AC makes with line AE 1mark
e) angle that plane BCGF makes with the base ABCD 2marks
10 marks
(a) A point a (35o N, 40oW) and b (40oS, 40oW), Calculate the distance between A and B in
Kilometers. Take earth radius o be 6370 km. answer to 1 d.p. (3mks)
(b) A and B are points on latitude 70oC. Their longitudes are 62oW and 118o E respectively. Find
the distance from A to B along a parallel of latitude. (4mks)
(c) Peter was in Mombasa 39oE and Mary was in Banju 17oW. Calculate the time difference
between the two. (3mks)
10 marks
ABCD is a quadrilateral with vertices as follows: A (3, 1), B (2, 4) C (4, 3) and D (5, 1)
(a) (i) On the grid provided draw the quadrilateral ABCD and the image A’B’C’D‘ under a
transformation With matrix 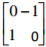
Describe the transformation that maps ABCD onto A’B’C’D’ fully (1mk)
(b) A transformation represented by the matrix 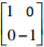
ordinates of A”B”C”D”. Plot A”B”C”D’‘ on the same grid. (3mks)
(c) Determine a single transformation that maps A”B”C”D” onto ABCD. Describe this
transformation fully. (3mks)
10 marks
The table below shows the income tax rates in Kenya.
| Income in K£ per month 1 – 325 326 – 975 976 – 1300 1301 – 1625 Over 1625 |
Rate in Ksh / K£ 2 3 5 6 7.5 |
(a) Mr. Sigei is a public servant who lives in a government house and pays a nominal rent of Ksh.
1220 per month. He earns a basic salary of Ksh. 24,800 and taxable allowances of Ksh.
13,380 per month. He is entitled to a monthly tax relief of Ksh. 1120. Calculate his monthly
i) Taxable income in K£. (2mks)
ii) Gross tax. (3mks)
iii) Tax due (2mks)
(b) Apart from income tax, the following monthly deductions are made from his salary.
i) HELB loan repayment Ksh. 2400
ii) NHIF Ksh 320
iii) 2% basic salary as union dues.
Calculate Mr. Sigei’s monthly net salary. (3mks)
10 marks
An airline has to fly 1000 passengers and 35000 kg of luggage from Nairobi to Kampala. Two
types of aircrafts are available. Type A takes 100 passengers and 2000 kg of luggage. Type B
takes 60 passengers and 3000 kg of luggage. The airline must not use more than 16 aircrafts
altogether.
(a) if the airline hires x type A aircrafts and y type B aircrafts, write down 3 inequalities to
represent the information above. (3mks)
(b) Draw the inequalities on a grid. (3mks)
(c) Find the minimum number of aircrafts the airline could use. (1mk)
(d) If the cost of hiring charges for each aircraft is sh 100,000 and sh 120,000 for type A and b
respectively, find:
(i) The number of planes of each type that should minimize the cost (2mks)
(ii) Minimum cost (1mk
10 marks
In a mathematics test, the probability of 3 students, Kamau, Otieno and Mwala passing are
⅔, ¾ and ⅚ respectively
(a) Draw a tree diagram to represent this information (3 marks)
(b) Use the tree diagram to find the probability that:
(i) All the three students will fail (2 marks)
(ii) At least two students will pass. (3 marks)
(iii) Only one student will pass (2 marks)
10 marks
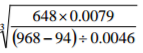
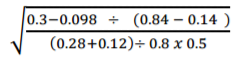


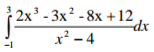


acha wee