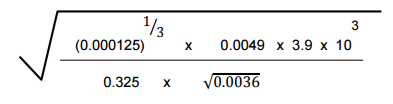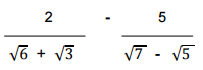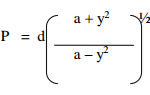KNEC KCSE Mathematics Paper 2 Question Paper / 2016 Pre KCSE
2016 Pre KCSE
Mathematics Paper 2
SECTION I (50 Marks)
Answer all the questions in this section in the spaces provided.
Evaluate without using tables or a calculator
4 marks
Find the value of the term independent of x in the expansion of
3 marks
Simplify the following giving your answer in the simplest form possible.
3 marks
Without using tables or a calculator evaluate
3 marks
Given that 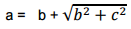
3 marks
Two matrices A and B are such that
Given that the determinant of AB = 4 find the image of triangle ABC where
A = (2,0) , B (3,2) and C (3,4) under stretch, stretch factor K, parallel to the
X axis.
3 marks
a. Find the position vector OC of the centre of a circle C, whose equation is
2x2 + 2y2 + 4x – 6y – 26 = 0 (2mks)
b. If the circle passes through P (3, 2), use vector method to find the diameter
of the circle. (2mks)
4 marks
The sum of the digits in a three digit number is nine. The tens digit is half the
sum of the sum of the other two and the hundreds digit is half the units digit.
Find the total value of the number.
3 marks
Find the exact area of the region bounded by the curve y = 9x – x3 and the x axis.
4 marks
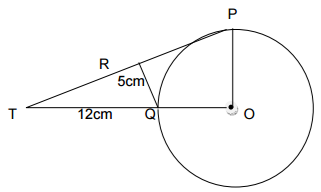
In the figure below, RP and RQ are tangents to the circle centre O, radius r cm. OQ produced meets PR produced at T. QT = 12cm and QR = 5cm
Calculate the radius of the circle.
3 marks
The figure below represents a right pyramid with a vertex V and a rectangular
base, ABCD. VA = VB = VC = VD = 40 cm.
AB = 30cm and BC = 22cm. X is the mid-point of BC.
Calculate the size of the angle between planes VBC and ABCD
3 marks
Given that a = 3i – 2j + 3k and
b = 2i – 4j – 3k
Find |2a – 3b|
3 marks
If 25x2 + k + 9 is a perfect square find x
2 marks
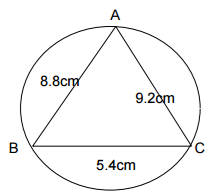
The figure below shows a circle centre O touching the vertices A , B , C
of triangle AB = 8.8cm , BC = 5.4cm and AC = 9.2cm.
Calculate the radius of the circle to the nearest whole number. (3mks)
3 marks
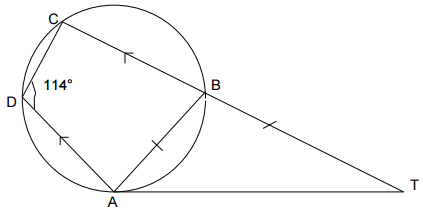
XAY is a tangent to the circle ABCD. AD is parallel to the straight line
CBY . Angle ADC = 114°, and AB = BY
Calculate angles
i. ABC (1mk)
ii. BCA (1mk)
2 marks
SECTION II (50 Marks)
Answer only five question in this section in the spaces provided.
The following table shows individual rates of income tax
| Income K£ 1 – 4512 4513 – 9024 9025 – 13536 13537 – above |
PA Rate (sh. Per K£) 2 3 4 5 |
Mr. Kariuki lives in a company house for which he pays a nominal rent of
Ksh.610 per month. For taxation purpose, his basic salary is increased by
15%. He is insured and pays sh.1200 as premiums per month and claims
insurance relief of K£ 36 per annum. He also claims a family relief of sh.660
per month. In addition, he is a member of a co-operative society, to which he
remits Ksh.1500 per month, as shares. If Mr. Kariuki’s P.A.Y.E is ksh.2400
per month, calculate his net salary in shillings per month.
2 marks
a. Using a ruler and a pair of compasses only construct
i. Triangle ABC, such that AB = 9cm, AC = 7cm and < CAB = 60° (2mks)
ii. The locus of P , such that AP ≤ BP (2mks)
iii. The locus of Q such that CQ ≤ 3.5cm
iv. Locus of R such that angle ACR ≤ angle BCR (2mks)
b. Find the area of the region satisfied by both P and Q (2mks)
10 marks
Points D(0° , 24°E) , E(O°, 21°W) , F(60°S, 120°W) , G(60°S, 110°E) are
marked in a globe representing the earth with radius = 0.7m.
(Taking π as 22/7 )
a. Find the length of the arc DE. (3mks)
b. If A is the centre of the latitude 60°S, and B is the centre of the latitude O° find
i. the length AB (3mks)
ii. the area of the major sector AFG (4mks)
10 marks
In a group of 40 people, 10 are healthy and every person of the remaining 30
has either high blood pressure, a high level of cholesterol or both. 15 have
high blood pressure and 25 have high level of cholesterol. If a person is
selected at random from this group, what is the probability that he/she
a. Has high blood pressure only (4mks)
b. Has high level of cholesterol only (2mks)
c.. Has high blood pressure and high level of cholesterol (2mks)
d. Has either high blood pressure or high level of cholesterol (2mks)
10 marks
Three consecutive terms in a G.P are 3 2x + 1 , 9x and 81 respectively.
a. Calculate the value of x (2mks)
b. Find the common ratio of the series. (2mks)
c. Calculate the sum of the first 10 terms of the series. (3mks)
d. Given that the 5th and 7th terms of the G.P in (a) above form the 1st two
consecutive terms of an A.P Calculate the sum of the 1st 20 terms of the
A.P. (3mks)
10 marks
Two variables y and x are believed to be related by the equation
y = x + ax b. The table below shows the corresponding values of x and y.
| x | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| y | 7.54 | 9.33 | 11.00 | 12.59 | 14.12 | 19.90 | 27.23 |
a. By drawing a suitable line graph, estimate the values of a and b. (9mks)
b. Write down the equation connecting y and x. (1mk)
10 marks
The marks obtained by fifty candidates were recorded in the table below.
| Marks | 0 – 9 | 10 – 19 | 20 – 29 | 30 – 39 | 40 x 49 | 50 – 59 | 60 – 69 |
| No. of candidates |
| | | | | | |
a. Draw a cumulative frequency graph and use it to estimate. (3mks)
i. Median (1mk)
ii. Quartile deviation (2mks)
iii. The percentage number of candidates failing if the pass mark was 25 marks.
(2mks)
iv. The range of marks scored by the middle 30% of the candidates. (2mks)
10 marks
A theatre has a seating capacity of 250 people. The changes are sh.100 for
an ordinary seat and sh.160 for a special seat. It costs sh.16,000 to stage a
Show and the theatre must make a profit. There are never more that 200
ordinary seats and for a show to take place, at least 50 ordinary seats must
be occupied. The number of special seats is always less than twice the
number of ordinary seats.
a. Taking x to be the number of ordinary seats and y the number of special
seats, write down all the inequalities representing the information above.
(4mks)
b. On a graph paper, show the region represented by the above inequalities.
(4mks)
c. Determine the number of seats of each type that should be booked in
order to maximize profit. (2mks)
10 marks