KNEC KCSE Mathematics Paper 2 Question Paper / 2015 KCSE Kericho West Joint Examination

Without using mathematical tables or a calculator, evaluate.2 𝑙𝑙𝑙𝑙𝑙𝑙3144 + 𝑙𝑙𝑙𝑙𝑙𝑙3972

Two variable V and R are such that V partly varies as R and partly varies as the square root of R. When R=9, V=144 and when R=16, V=272
a) Find the law connecting V and R (3 marks)
b) Hence find the value of V when R=56.25. (1 mark)

Make n the subject of the formula given that
𝐸𝐸 = �𝑥𝑥(𝑛𝑛2 − 𝑥𝑥)
𝑛𝑛2 − 1

A shopkeeper bought x kg of locally made sugar at Kshs 85 per kilogram and 120kg of imported sugar at ksh 102 per kilogram. He mixed the two types of sugar and sold the mixture at Ksh 119 per kilogram making a profit of 25%. Find the number of kilograms (x) of locally made sugar.

In the figure below AB and Bc are chords of a circle centre O. AB=6cm, BC=16cm and OC=10cm
Calculate angle ABC correct to three significant figures.

Kamau saved 2000 during the first month of employment. In each subsequent month he saved 15% more than the preceding month. How many years did he take to save a sum of Kshs 2.028,692.

Given that 𝐴𝐴 = 2𝑖𝑖 + 𝑗𝑗 − 2𝑘𝑘, 𝐵𝐵 = 3𝑗𝑗 + 4𝑗𝑗 − 𝑘𝑘 𝑎𝑎𝑎𝑎𝑎𝑎 𝐶𝐶 = −5𝑖𝑖 + 3𝑗𝑗 + 2𝑘𝑘 𝑎𝑎𝑎𝑎𝑎𝑎 𝑡𝑡ℎ𝑎𝑎𝑎𝑎 𝑃𝑃 = 3𝐴𝐴 − 𝐵𝐵 + 2𝐶𝐶, Find the magnitude of the vector P to three significant figures.

Solve the equation 2𝐶𝐶𝐶𝐶𝐶𝐶3𝜃𝜃 = √3 𝑓𝑓𝑓𝑓𝑓𝑓 00 ≤ 𝜃𝜃 ≤ 1800

There are two boxes A and B on the floor. Box A contains 3 red marbles and 5 white marbles while Box B contains 6 red marbles and 2 white marbles. A box is chosen at random and two marbles are drawn from it one after the other without replacement. Find the probability that the two marbles are of different colours.

Without using mathematical tables or a calculator evaluate.
𝑆𝑆𝑆𝑆𝑆𝑆1500 + 𝐶𝐶𝐶𝐶𝐶𝐶2100
𝑇𝑇𝑇𝑇𝑇𝑇 2250 − 𝑇𝑇𝑇𝑇𝑇𝑇2400

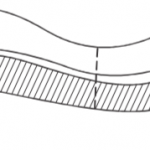
In the figure below ABT is straight line with AB=5cm and BT=4cm. O is the centre of the circle with radius 8 cm and PT is a tangent to the circle at P.
a) Calculate the length of PT. (1 mark)
b) Calculate the area of the shaded region correct to two significant figures (Take π = 3.142 (3 marks)

a) Expand (𝑎𝑎 + 𝑏𝑏)5 (1 mark)
b) Use the first three terms of the expansion in (a) to find the value of (1.97)5 to two decimal places. (2 marks)

Given that 10.5 ≤ 𝑥𝑥 ≤ 20 𝑎𝑎𝑎𝑎𝑎𝑎 1.5 ≤ 𝑦𝑦 ≤ 3, find the maximum value and correct to three decimal places of: 𝑥𝑥−𝑦𝑦
𝑦𝑦+𝑥𝑥

Two matrices A and B are A=�
𝑃𝑃 4
3 2
� and B�
1 2
3 4
� Given that the product AB is a singular matrix, find the value of P.

A (-6,-2) and B (2,-4) are the end point of a diameter of a circle.
Find the co-ordinates of the centre of the circle (1 mark)
Find the equation of the circle expressing it in the form 𝑥𝑥2 + 𝑦𝑦2 + 𝑎𝑎𝑎𝑎 + 𝑏𝑏𝑏𝑏 + 𝑐𝑐 = 0, 𝑤𝑤ℎ𝑒𝑒𝑒𝑒𝑒𝑒 𝑎𝑎, 𝑏𝑏 𝑎𝑎𝑎𝑎𝑎𝑎 𝑐𝑐 𝑎𝑎𝑎𝑎𝑎𝑎 intergers.

A farmer has 200m of fencing with which to form three sides of a rectangular enclosure, the fourth side being existing wall of the yard. Find in metres the dimension of the largest possible area that can be enclosed.

Mr. Korir borrowed Kshs 3,600,000 from the bank to buy a residential house. He was required to repay the loan with a
simple interest for a period of four years. The repayment amounted to kshs 111 000 per month. Calculate
a) i) the interest paid to the bank. (2 marks)
ii) the rate per annum of the simple interest. (2 marks)
b) The value of the house appreciated at the rate of 15% per annum. Calculate the value of the house after 4 years to the
nearest hundreds. (3 marks)
c) After n years, the value of the house was Kshs 8,327,019. Find the value of n. (4 marks)

A certain number of Jua kali artisan agreed to contribute equally to buy a welding machine worth Ksh 12,000. Five of the artisan pulled out so the others agreed to contribute an extra Kshs 100 each. Their contribution enabled them to buy a machine worth Ksh 2000 more than the previous machine.
a) If the original number of artisan was n, write down:
i) An expression of how much each artisan was to contribute originally. (1 mark)
ii) An expression of how much each of the remaining artisan contributed. (1 mark)
b) Calculate how many artisan made the contribution. (6 marks)
c) Calculate how much each contributed. (2 marks)

In the figure below AOC is a diameter, ADG and BCFG are straight lines, angle ACB=420, angle CAE=740 and angle
DEC=360
Find the following angles, giving reasons in each case.
a) Angle CDE (2 marks)
b) Angle BDC (2 marks)
c) Angle DCA (2 marks)
d) Reflex angle COE (2 marks)
e) Angle DGF (2 marks)

a) Copy and complete the given table below to 2 decimal places. (2 marks)
𝑥𝑥0 00 300 600 900 1200 1500 1800 2100 2400 2700
𝑆𝑆𝑆𝑆𝑆𝑆(𝑥𝑥 + 300) 0.50 0.87 0.50 -0.50 -1.00 -0.87
𝐶𝐶𝐶𝐶𝐶𝐶 (𝑥𝑥 − 150) 0.97 0.71 -0.26 -0.71 -0.97 -0.71
b) Using the same axes plot the curves y=Sin(x+300) and y=Cos (x-15) (5 marks)
Taking 1 cm represented 300 and x-axis and 1cm represented 0.25cm on the y axis.
c) Using the graph state the amplitude of y=Cos (x-150) (1 mark)
d) Using the graph solve the equation: Sin (x+300)-Cos (x-150)=0 (2 marks)

The figure below shows a frustrum ABCDEFGH of a right pyramid where AB=40cm, BC=30cm, FG=20cm, GH=15cm
and AF=BG=CH=DE=25cm.
Find the vertical height of the frustrum. (3 marks)
a) Find the angle between line BE and the base ABCD (2 marks)
b) Find the angle between the plane BCHG and the base ABCD. (2 marks)
c) Find the angle between the plane ADEF and the plane AGHD (3 marks)

a) Using a ruler and pair of compasses only construct a square ABCD of sides 6cm. (2 marks)
b) A point P moves inside the square such that;
i) 𝐴𝐴𝐴𝐴 ≤ 𝑃𝑃𝑃𝑃
ii) 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 𝐴𝐴𝐴𝐴𝐴𝐴 ≥ 900
iii) P is nearer to AD than AB. construction on the square in (a) show the region that P must lie by shading.
c) Find the area of the region where P must lie. (2 marks)

A ship leaves an Island A (600N, 450E) and sails due west for 120hours to another island B.The average speed of the ship is 27 knots.
a) Find the position of the island B (4 marks)
b) Another island C is south of island B and lies on latitude 550N. Find the distance between Islands B and C in nautical miles. (2 marks)
c) The ship leaves island B when the time at Island A is 12.30pm. On Monday and sailed to Island C. If the ship increases its speed by 20% between B and C find out the time of arrival at island C to the nearest minutes and the day. (4 marks)

a) Complete the table below for the equation 𝑦𝑦 = 2𝑥𝑥3 + 5𝑥𝑥2 − 𝑥𝑥 − 6
x -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
𝑦𝑦 = 2𝑥𝑥3 + 5𝑥𝑥2 − 𝑥𝑥 − 6 -12 0 -2 -6 0 28
b) On the grid provided draw the graph 𝑦𝑦 = 2𝑥𝑥3 + 5𝑥𝑥2 − 𝑥𝑥 − 6 𝑓𝑓𝑓𝑓𝑟𝑟 − 3.5 ≤ 𝑥𝑥 ≤ 2. Use 2cm to represent 1 unit
on the x-axis and 1cm to represent 5 units on the y-axis. (3 marks)
c) By drawing a suitable line use the graph in (b) to solve the equation. (5 marks)
2𝑥𝑥3 + 5𝑥𝑥2 − 3𝑥𝑥 − 4 = 0