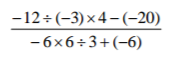KNEC KCSE Mathematics Paper 1 – 2014 KCSE COMA Joint Exam
2014 KCSE COMA Joint Exam
Mathematics Paper 1
SECTION 1 (50 Marks)
Answer all questions in this section.
Evaluate:
3 marks
An airbus left Nairobi at 1945hrs and arrived in London at 0320hrs. It stayed for 112 hrs for rest and refreshment of passengers and crew. It then headed for Washington D.C and took 1014 hrs.
(a) How long did the journey from Nairobi to London take in hours and minutes? (2 marks)
(b) At what time did it arrive in Washington D.C. (2 marks)
4 marks
Evaluate:
3 marks
In the Kapsabet station church choir, the ratio of male to female is 2:3. On one Sunday service,
10 male members were absent and six new female members joined the choir as guests for that day.
If on this day the ratio of males to females was 1:3, how many regular members does the choir have?
3 marks
The figure below represents a roof truss symmetrical about QS. Beam PQ is 5m long and strut TS
is 2.4m long. The distance TQ is 1.8m.
Calculate:-
(i) the height QS. (2 marks)
(ii) hence, find the span PR of the roof. (2 marks)
4 marks
n article was bought at Ksh.2250 then later sold for Ksh.2520. Calculate:-
(i) the percentage profit. (2 marks)
(ii) the price at which it should be sold to make a profit of 20%. (2 marks)
4 marks
In a rectangle ABCD, the side AB has equation 3x+ 2y = 6 and vertex D has coordinates (-2, 4).
Find the equation of side AD in the form ax+ by = C. Where a, b and C are integers.
3 marks
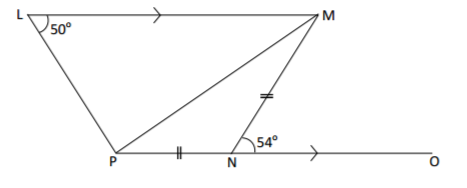
In the figure below MNO = 54º and PLM = 50º, PN = NM and PO is parallel to LM.
Find the value of LPM.
3 marks
Using ruler and pair of compass only, construct triangle ABC in which AB = 6cm, BC = 8cm and
angle ABC = 45º. Drop a perpendicular from A to meet BC at M. Measure AM and AC.
3 marks
A plane leaves town P to town Q on a bearing of 130º and a distance of 350km. it then flies
500km on a bearing of 060º to town R. Find, by scale drawing the distance between town R and
town P.
3 marks
Use tables of reciprocal and squares to evaluate, to 4 significant figures, the expression:
0.43462+127.46
3 marks
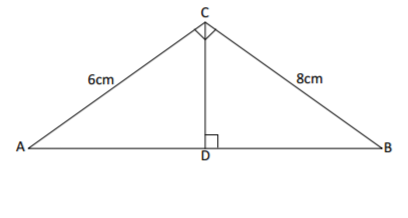
The figure below shows a triangle ABC which is right-angled at C. CB = 8cm and AC = 6cm.
Find the length of CD given that CD is perpendicular to AB.
3 marks
Solve for t in the equation:
32(t-3)÷8(t-4)=64÷2t
3 marks
A is a reflex angle and tan A = 724 . Determine the value of Cos A without using the Mathematical
table or calculator. (2 marks)
2 marks
Translation T is represented by the column vector 

If point R is at (7, – 4), determine the coordinates of point P.
3 marks
(i)On the grid provided, (i) Plot the points P (4, -1), Q (5, -3), R (4, -4) and S (3, -3) and join the
points to form a polygon PQRS. State the name of the polygon formed. (2 marks)
(ii) Write down the equation of the line of symmetry of the polygon. (1 mark)
3 marks
SECTION II (0 Marks)
Answer any FIVE questions in this section.
The capacity of two similar rectangular tanks are 1,000,000 litres and 512,000 litres respectively.
(a) Determine the length of the larger tank if the smaller one is 240cm long. (4 marks)
(b) Calculate the surface area of the smaller tank if the larger tank’s surface area is 1875m². (3 marks)
(c) Estimate the mass of the smaller tank if the mass of the larger one is 800kg. (3 marks)
10 marks
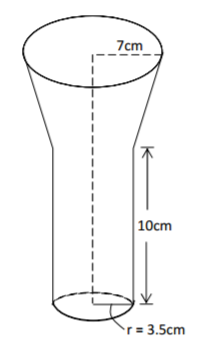
The diagram below represents a model of a pillar. The radii of the top and the base are 7cm
and 3.5cm respectively. The height of the cylindrical part is 10cm while the height of the whole
pillar is 15cm.
(a) Calculate the volume of the model in cm³. (6 marks)
(b) Calculate the mass of the material used to construct the pillar given that the actual height of the
whole pillar is 60m and the density of the material used is 0.832g/cm³. (Give your answer in tones).
(4 marks)
10 marks
(a) Use the quadratic formula to solve the equation 2x2 – 9x + 3 = 0 giving your answer to 4 significant figures. (3 marks)
(b) Simplify the expression completely: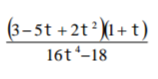
(c) If the expression 25y² – 70y + (16 + K) is a perfect square; where K is a constant;
find the value of K. (3 marks)
10 marks
Christians who attended a church service on a Sunday were grouped by age as shown in the table
below.
| Age in x years | 0<x<5 | 5<x<15 | 15<x<25 | 25<x<45 | 45<x<75 |
| No. of members | 14 | 41 | 59 | 70 | 15 |
(a) Estimate the mean age (4 marks)
(b) On the grid provided, draw a histogram to represent the distribution. Use the scale:
- 1cm to represent 5 units on the horizontal axis.
- 2cm to represent 5 units on the vertical axis. (4 marks)
(c) On the same axes in (b) above, construct a frequency polygon and use it to determine the modal
class. (2 marks)
10 marks
Nairobi and Eldoret are each 250km from Nakuru. At 8.15a.m, a lorry leaves Nakuru for Nairobi.
At 9.30am, a car leaves Eldoret for Nairobi via Nakuru at a speed of 100km/h. Both vehicles arrived
Nairobi at the same time.
(a) Calculate their time of arrival in Nairobi. (2 marks)
(b) Find the cars speed relative to that of the lorry. (4 marks)
(c) How far apart are the vehicles at 12.45pm. (4 marks)
10 marks
Complete the table below, for the function y=-x2+2x+6. (2 marks)
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| –x2 | _ | _ | 0 | _ | _ | _ | _ | _ | _ |
| 2x+6 | _ | _ | 6 | _ | _ | _ | _ | _ | _ |
| y | _ | _ | 6 | _ | _ | _ | _ | _ | _ |
(b) On the grid provided, draw the graph of the function y=-x2+2x+6.for the range -2< x<6
and use your graph to estimate the roots of the equation -t2 +2t+6=0 to 1 decimal place. (4 marks)
10 marks
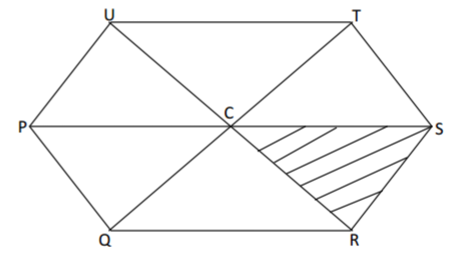
In the figure below, PQRSTU is a regular hexagon.
(a) Describe fully:
(i) a reflection that maps SCR onto STC. (1 mark)
(ii) an enlargement that maps SCR on PCU. (2 marks)
(iii) a rotation that maps SCR to TCU. (3 marks)
(b) The PQC is reflected on the line RU. The image of PQC under the reflection is then
rotated through an angle -120º about point C. Determine the images of P and Q:
(i) under the reflection. (2 marks)
(ii) after the two successive transformations. (2 marks)
10 marks
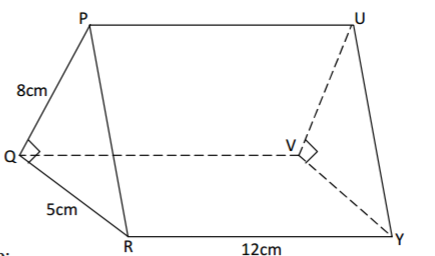
The figure below shows a wedge in which PQR and UXY are congruent right angled triangles.
PQ = 8cm, QR = 5cm and RY = 12cm.
(a) Calculate:
(i) the length of RU. (2 marks)
(ii) the angle the line RU makes with the plane PQVU. (2 marks)
(b) Find the angle between:-
(i) line PY and the plane QRYV. (3 marks)
(ii) the planes PQVU and PRYU. (3 marks)
10 marks