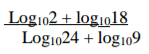KNEC KCSE Mathematics Paper 2 – 2014 Gatundu Mock
2014 Gatundu Mock
Mathematics Paper 2
SECTION I (50 Marks)
ATTEMPT ALL QUESTIONS IN THIS SECTION
Simply without using tables or calculators:
3 marks
Using a ruler, a set square and a pair of compasses only,
(a) Draw a line AB = 5cm (1 mark)
(b) Divide the above line into 9 equal parts. (2 marks)
3 marks
Simplify
4 marks
(a) Expand and simplify 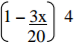
(b) Hence use the above expansion to evaluate (1.03)4 to 4 s.f (2 marks)
4 marks
A circle whose equation is (x – 1)2 + (y – k)2 + (y-k)2 = 10 passes through the point (2, 5). Find the
coordinates of the two possible centres of the circle.
3 marks
(a) Find the inverse of the matrix 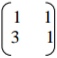
(b) Hence determine the point of intersection of the:
lines:
y + x = 7
3x + y = 15 (2 marks)
4 marks
Waiguru invested shs.6000 for 1 ½ years at 12% p.a compounded quarterly. Determine:
(a) The amount accruing at the end of 1 ½ years. (3 marks)
(b) Interest earned. (1 mark)
4 marks
Given that y2 is inversely proportional to x and y = 1.5 when x = 2/3, find the value of y when x = 6.
3 marks
A single unbiased dice is thrown once. Find the probability that the score will be:
(a) even (1 mark)
(b) a multiple of 3 (1 mark)
2 marks
Two types of tea which cost ksh.200 per kg and ksh 250 per kg are mixed so that their weights are in
the ratio 5:3 respectively. Calculate the cost of 20kg of the mixture.
3 marks
A plane flies from Cairo (40oN, 30oE) to Harare ( So, 30oE) a distance of 3,300nm. Determine the
latitude θSo.
3 marks
Find the percentage error in evaluating (x + y) – z ; if x = 3.2cm, y = 5.6cm and z = 2.4cm.
3 marks
Without using calculator or mathematical tables; Find the sums of the first 20 terms of the series:
log2 + log 4 + log 8 + log 16 + —————-
3 marks
Q represent a positive quarter turn about (0, 0) and R is the reflection in the line y-x=0. Find QR (2, 1)
3 marks
Find the acute angel y if cos 4y = sin 2y.
2 marks
In the diagram below, O is the centre of the circle SPQ. Angle SOQ = 130o
Calculate angle:
(a) ro (1 mark)
(b) po (2 marks)
3 marks
SECTION II (50 Marks)
ATTEMPT ANY 5 QUESTINS IN THIS SECTION
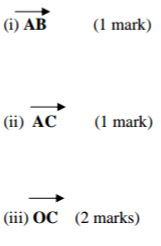
The vectors a and b are not parallel. Given that
(a) 3a + hb = ka + 2b. Find the values of the scalars h and k. (3 marks)
(b) The position vectors of points A and B relative to a point of origin O are a and b respectively. C
is the point on AB such that AC:CB = 5:3. Express in terms of a and b the vectors.
(c) (i) D is a point on OB such that OD = b. Express 
(ii) Find the value of ; if OA is parallel to DC. (1 mark)
10 marks
18. Complete the table below for graphs of:
y = 3 sin (2x – 30o) and y = sin x for -120o< x < 120o
(a) Correct to 2 d.p.
| xo | -120o | -90o | -60o | -30o | 0o | 30o | 60o | 90o | 120o |
| y=sin xo | -0.87 | -1.00 | -0.50 | 0 | 0.87 | 1.00 | |||
| y = 3sin (2x-30o) | 1.50 | -3.00 | -1.50 | 1.50 | 1.50 |
(b) On the grid provided; draw the graphs on the same axes of: y = sin x and y = 3 sin (2x – 30o) (4 marks)
Take the scale: 1cm for 15o on x-axis and 2cm for 1 unit on the y-axis.
(c) State the amplitude and period of each wave. (2 marks)
(d) Find the value of x: for which Sin (2x – 30o) – 1/3 sin x = 0. (2 marks)
10 marks
The heights to the nearest centimeter of 100 boys were recorded as shown below
| Heights | 140-145 | 146-151 | 152-157 | 158- 163 | 164-169 | 170-75 | 176-181 | 182-187 | 188-193 | 194-199 |
| Frequency | 3 | 4 | 7 | 10 | 10 | 15 | 25 | 16 | 8 | 2 |
Using an assumed mean of 166.5
(a) Calculate the mean (5 marks)
(b) The variance (3 marks)
(c) The standard deviation (2 marks)
10 marks
P and V are connected by the law P = KVn where k and n are constants. The table below shows values
of P and V.
| V | 2 | 2.3 | 3 | 3.5 | 4 |
| P | 288 | 503.7 | 1458 | 2701 | 4608 |
| _ | _ | _ | _ | _ | _ |
| _ | _ | _ | _ | _ | _ |
(a) Express P = KVn in linear form. (1 mark)
(b) Complete the table and draw a linear graph to represent the information given above. (4 mark)
(c) Find the values of k and n (2 marks)
(d) Find the law connecting p and v. (1 mark)
(e) Find the value of p when v = 6. (2 marks)
10 marks
An institute offers two types of courses, veterinary and Agriculture. The institute has a capacity of 500 student. There must be more Agriculture students than Veterinary students. At least 200 students must take veterinary courses. If x represent the number of veterinary students and y the numbers of
Agriculture students.
(a) Write down three inequalities that describe the given conditions. (3 marks)
(b) On the grid provided, draw the three inequalities. (3 marks)
(c) If the institute makes a profit of shs.25,000 to train one veterinary student and shs. 10,000 to
train one Agriculture student, determine:
(i) The number of students that must be enrolled in each course to maximize the profit.
(2 marks)
(ii)The maximum profit. (2 marks)
10 marks
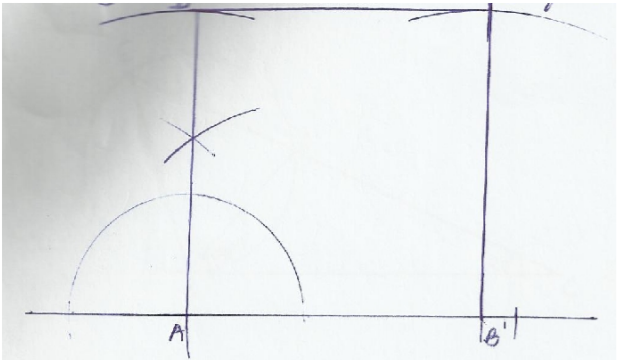
Use a ruler and compasses only in this question.
The diagram below shows a square ABCD.
(a) Construct two circles with centre O, with one passing through the vertices ABCD and the other one,
touching the four sides of the square ABCD (4 marks)
(b) (i) Locate point P if BPC is the tangent of the smaller circle. (1 mark)
(ii)Show the locus of a point T inside the square such that <APB = <ATB (3 marks)
(c) (i) Point Q is the point where the locus b(ii) above meets side AD. Label the locus of point Q.
(1 mark)
(ii) Shade the locus of a region R inside the square such that <QRP 90o and above the locus of point T. (1mark)
10 marks
In the figure below Angle CBD = 37o, angle BCD = 20o and ABC is a tangent to the circle at B.
(a) Find:
(i) Angle BED (2 marks)
(ii) Angle ABE (1 mark)
(iii) Angel BDC (1 mark)
(b) With reasons state whether triangle BDC is similar to triangle CBE. (2 marks)
(c) Given that the radius of the circle is 2.5 cm and the length BC= 6cm, find the length EC using the
cosine rule. (4 marks)
10 marks
The displacement in metres of a particle from a point O after t seconds is given by s=t(t-2)t-1); Find :
(a) The speed of the particle when t = 2 seconds. (3 marks)
(b) Its minimum speed. (2 marks)
(c) The time when the particle is momentarily at rest. (3 marks)
(d) It acceleration when t = 3 seconds. (2 marks)
10 marks